Kunnskapsbasertpraksis.no
Kunnskapsbasert praksis
Sist faglig oppdatert: 17.09.2021

Er du kliniker, lærer eller student i medisin og helsefag? Her kan du lære å finne, vurdere og bruke forskningsbasert kunnskap i praksis.
Kunnskapsbasert praksis innebærer at fagutøvere bruker ulike kunnskapskilder i praksis. Ved å bruke forskningsbasert kunnskap, erfaringer fra praksis og pasientens kunnskap og behov bedrer vi kvaliteten på tjenestene våre.
Kunnskapsbasert praksis (KBP) er å ta faglige avgjørelser basert på systematisk innhentet forskningsbasert kunnskap, erfaringsbasert kunnskap og pasientens ønsker og behov i en gitt situasjon.

Vi henter kunnskap fra ulike kilder, for eksempel fra kollegaer, eksperter, forskning, retningslinjer, kurs osv. Disse kildene har styrker og svakheter. Vi som arbeider i klinisk praksis, må være bevisst på disse styrkene og svakhetene. KBP kan hjelpe deg med å øke bevisstheten om og reflektere over hvilke kunnskapskilder du baserer dine handlinger på.
Hvorfor jobbe kunnskapsbasert?
Formålet med kunnskapsbasert praksis er å styrke beslutningsgrunnlaget til deg som jobber i helse- og sosialsektoren, og bevisstgjøre hvor du henter din kunnskap fra. Prosedyrer som ikke er basert på oppdatert kunnskap kan i verste fall føre til feilbehandling av pasienter. Derfor er det viktig at helsepersonell lærer seg metoder for hvordan de skal søke seg fram til den beste tilgjengelige kunnskapen og kritisk vurdere denne.
Gro Jamtvedt, OsloMet – storbyuniversitetet, gir deg en innføring i kunnskapsbasert praksis (KBP). Gro underviser i KBP og har skrevet lærebøker om emnet (5:23 min):
Arild Bjørndal, tidligere direktør ved Regionssenter for barn og unges psykiske helse, gir informasjon om hvorfor kunnskapsbasert praksis er viktig. Arild har motivert helsepersonell til å arbeide kunnskapsbasert siden starten av 1990-tallet (5:53 min):
Trinnene i kunnskapsbasert praksis
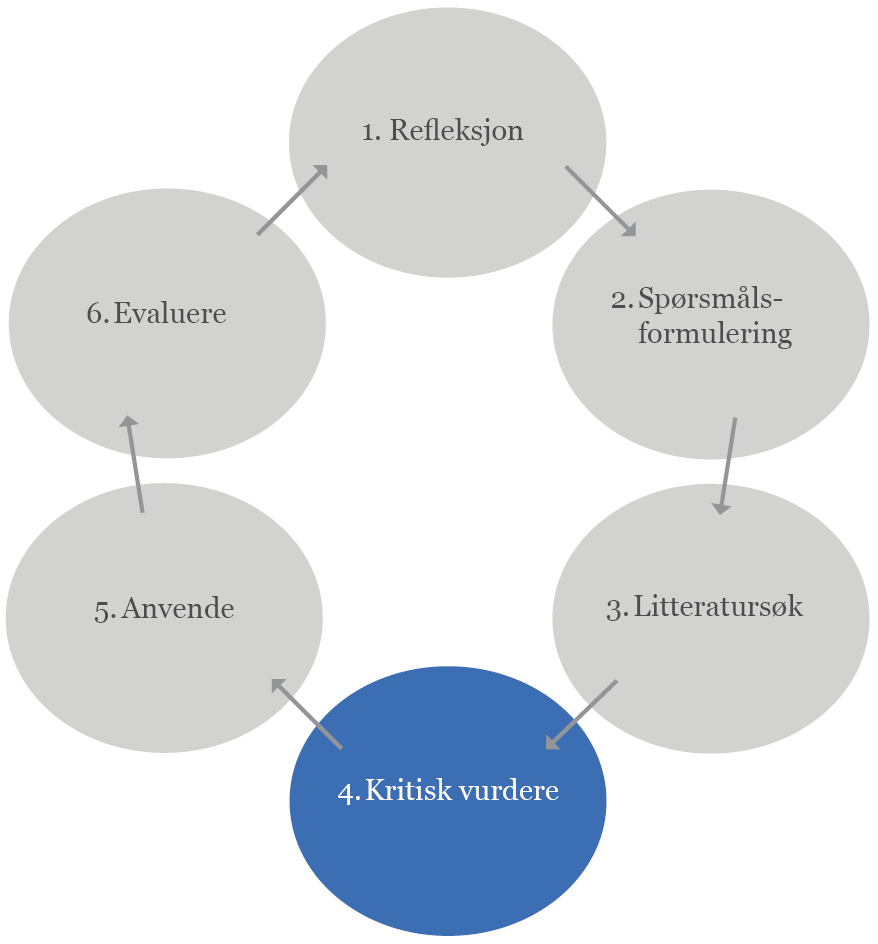
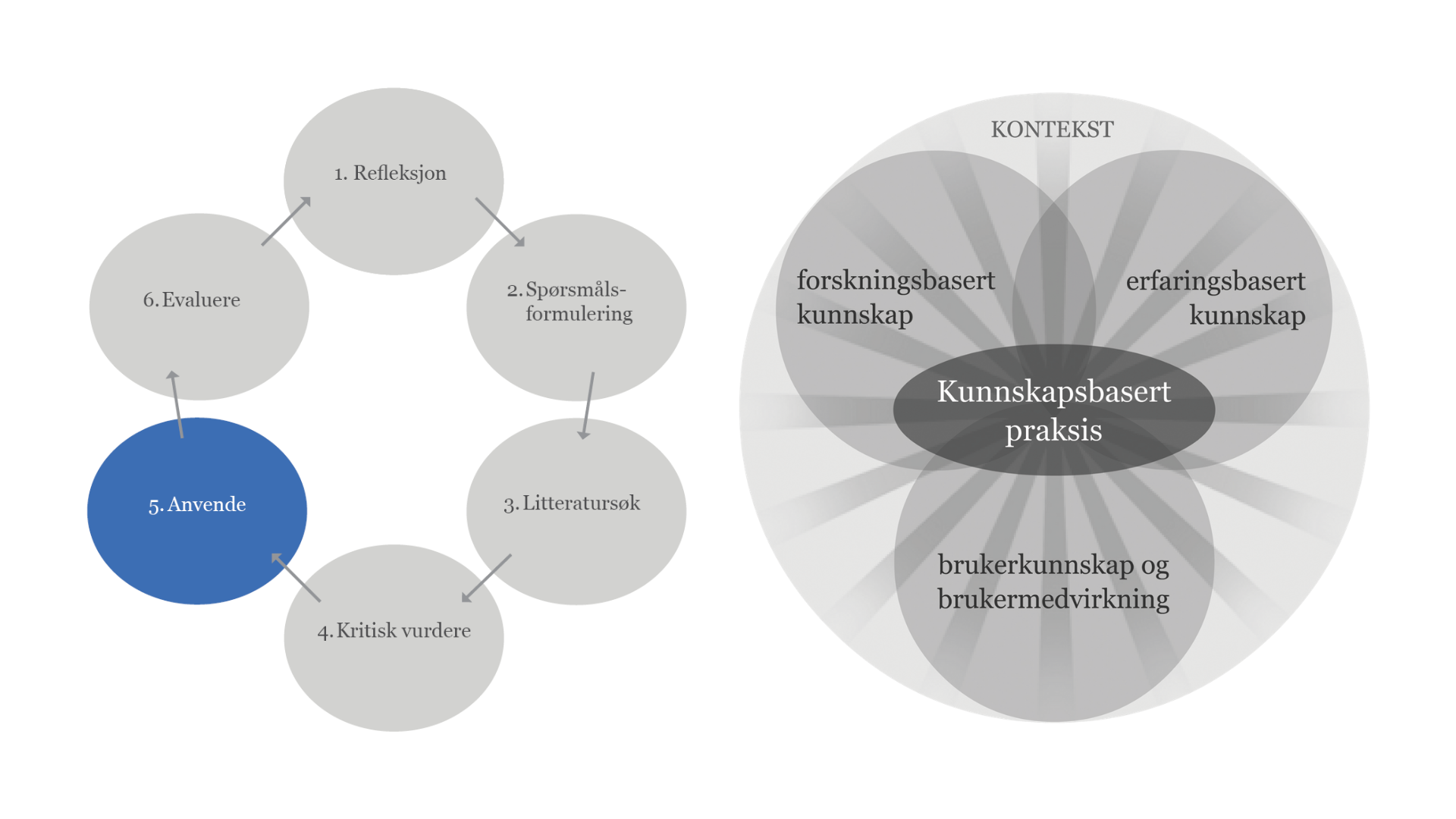
Kunnskapsbasert praksis presenteres gjerne som en prosess i seks trinn. Hvert trinn er viktig i ditt daglige arbeid.
Trinnene i kunnskapsbasert praksis:
- Refleksjon over egen praksis
- Formulere spørsmål (spørsmålsformulering)
- Finne forskningsbasert kunnskap (litteratursøk)
- Kritisk vurdere forskningen
- Anvende forskningsbasert kunnskap med erfaringsbasert kunnskap og brukerens behov
- Evaluere egen praksis
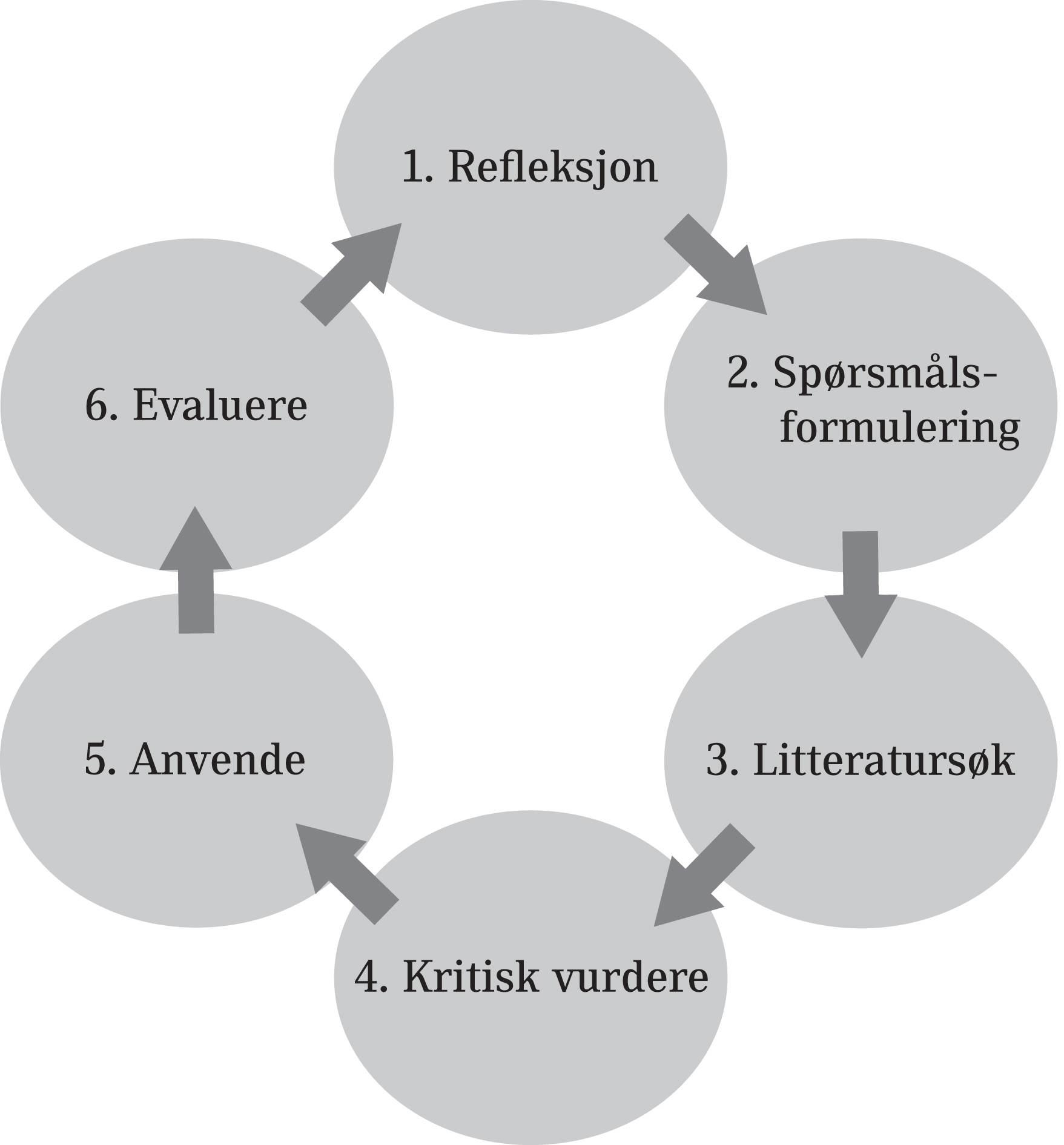
Hva går egentlig det enkelte trinn ut på? Kristine Berg Titlestad, Høgskulen på Vestlandet, presenterer trinnene i denne videoen som er laget for prosjektet KBP på tvers (3:23).
1. Refleksjon over egen praksis
Sist faglig oppdatert: 29.09.2021
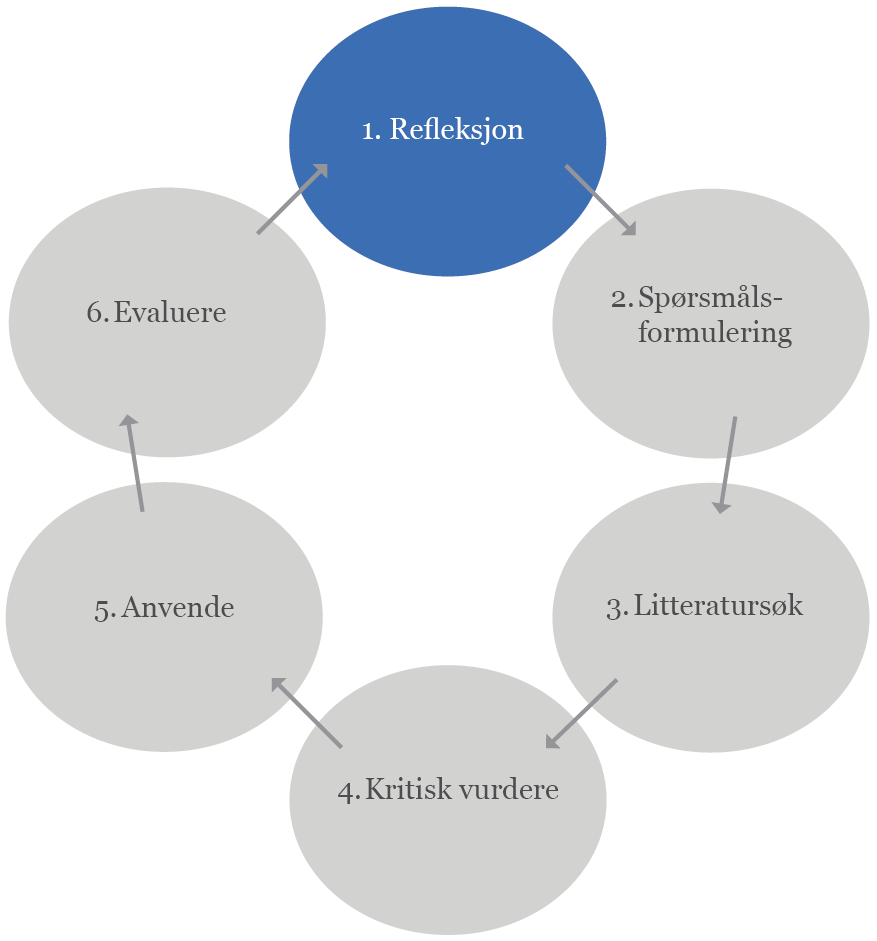
Tenk deg at du jobber på en sengepost der pasientene har kirurgiske sår. Hvordan man steller slike sår kan variere fra arbeidsted til arbeidssted og mellom sykepleiere på samme arbeidssted. Når det kommer nyansatte læres de gjerne opp av erfarne sykepleiere som gjør det på "sin måte". Dette innebærer at det kan være stor variasjon i praksis.
I slike situasjoner er det viktig å stille seg en del spørsmål, for eksempel:
- Hvorfor gjør noen det på en måte mens andre gjør det på en annen måte?
- Hva betyr det for pasientene at det gjøres på forskjellige måter?
- Er den ene metoden bedre enn den andre?
I det hele tatt er det viktig å spørre seg om hvorfor vi gjør det vi gjør. Diskuterer vi med kollegaer hva som er grunnlaget for beslutninger i vår fagutøvelse? Er det kultur på arbeidsplassene for å stille spørsmål om hva vi gjør? Legger ledere til rette for refleksjon?
I denne videoforelesingen snakker fysioterapeut Nina Rydland Olsen ved Høgskulen på Vestlandet om hvordan reflektere over egen praksis (5:06).
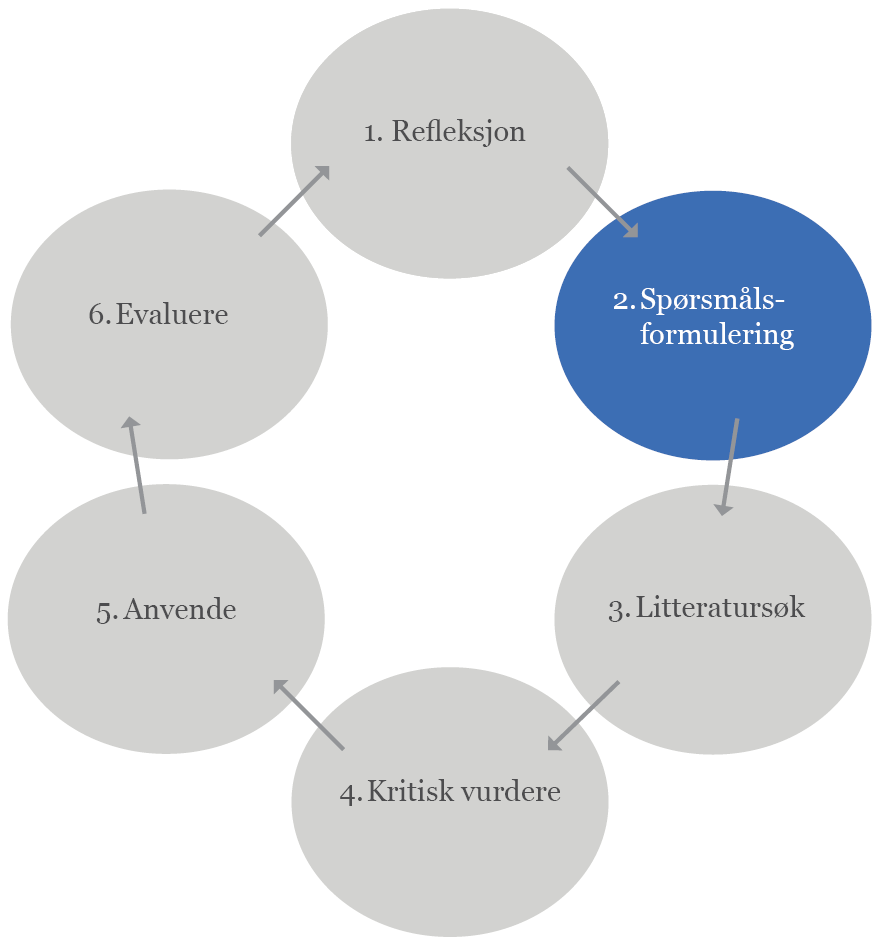
2. Spørsmålsformulering
Sist faglig oppdatert: 09.06.2017
Et viktig prinsipp i kunnskapsbasert praksis er å bruke relevant forskning på spørsmål som er pasient- og praksisnære. Når du står overfor et problem i praksis må du formulere et presist spørsmål for å kunne søke frem relevant forskning og finne svar på spørsmålet. Et presist spørsmål er et godt utgangspunkt for et vellykket litteratursøk.
Et presist spørsmål bør inneholde informasjon om hvem vi er interessert i, hvilke tiltak vi er interessert i og hvilke utfall som er av interesse.
PICO er et nyttig verktøy for å formulere presise spørsmål. Når du har et klart formulert spørsmål, bør du definere hvilken type kjernespørsmål det er ettersom ulike typer av kjernespørsmål besvares med ulike forskningsmetoder eller studiedesign.
2.1 PICO
Sist faglig oppdatert: 30.09.2021
I kunnskapsbasert praksis er det viktig å gjøre spørsmålet (problemstillingen) tydelig og presist. PICO og PICo er verktøy som hjelper deg med dette. Når du har formulert et presist spørsmål bør du bestemme hvilket kjernespørsmål du står overfor. Dette vil hjelpe deg når du skal søke etter forskning om ditt spørsmål.
PICO gir struktur og klargjør spørsmålet for litteratursøk, utvelgelse og kritisk vurdering av litteraturen. PICO er en forkortelse for elementer som ofte vil være med i et spørsmål.
| P | Population/problem | Hvilken populasjon eller hvilket problem dreier det seg om? |
| I | Intervention | Hva er det med denne populasjonen eller dette problemet du er interessert i? Er det tiltak som er iverksatt (intervensjon) eller noe populasjonen blir utsatt for (eksponering)? |
| C | Comparison | Ønsker du å sammenligne to typer tiltak? I så fall skal det andre tiltaket stå her (f.eks. dagens praksis). |
| O | Outcome | Hvilke utfall eller endepunkter er du interessert i? |
Ønsker du mer informasjon om verktøyet PICO? Birgitte Graverholt, Høgskulen på Vestlandet, forklarer PICO og bruker eksempler for å vise hvordan du kan ha nytte av PICO i praksis. Birgitte underviser i KBP og forsker på hvordan KBP fungerer ute i klinisk praksis (4:40 min).
Mens PICO er godt egnet for spørsmål som besvares med kvantitative forskningsdesign, er PICo med liten o mer egnet til spørsmål som besvares med kvalitativ forskningsmetode, for eksempel spørsmål om opplevelser og erfaringer
| P | Population/problem | Hvilken populasjon eller hvilket problem dreier det seg om? |
|---|---|---|
| I | (Phenomenon of) Interest | Hvilken aktivitet, erfaring, opplevelse eller prosess dreier det seg om? |
| Co | Context | Hvilken kontekst eller setting dreier det seg om? |
2.2 Kjernespørsmål
Sist faglig oppdatert: 14.11.2020
Når du har formulert et klart spørsmål utfra problemstillingen anbefaler vi at du definerer hvilket kjernespørsmål det hører inn under. Et kjernespørsmål hjelper deg å finne ut hvilken forskningsmetode som gir pålitelige svar på ditt spørsmål og hvor du finner denne forskningen.
Spørsmål fra klinisk praksis kan kategoriseres i følgende seks kjernespørsmål:
| Kjernespørsmål | Kunnskap |
| Hvor mange har et helseproblem? | Prevalens – forekomst |
| Hvorfor får noen dette problemet, mens andre holder seg friske? | Årsak – etiologi |
| Hvordan kan vi avgjøre om noen har dette problemet? | Diagnostikk |
| Hva kan gjøre for å forebygge eller behandle problemet? | Effekt av tiltak |
| Hvordan går det med den som har problemet? | Prognose - sykdomsforløp |
| Hvordan oppleves det? Hva er det som gjør at det virker? |
Erfaringer og holdninger |
Ønsker du mer kunnskap om kjernespørsmål? Per Olav Vandvik, Universitetet i Oslo, Lovisenberg sykehus og Folkehelseinstituttet, gir deg en oversikt over ulike typer kjernespørsmål i helsetjenesten og innsikt i hvorfor det er viktig å skille disse fra hverandre. (5:20 min):
2.3 Forskningsmetode
Sist faglig oppdatert: 14.11.2020
Hvilken metode som brukes i forskning kalles gjerne forskningsdesign eller forskningsmetode. Hvilke type kjernespørsmål du har avgjør valg av forskningsmetode. Tabellen under beskriver kjernespørsmål i helsetjenesten, hvilken kunnskap de kan gi, og hvilken forskningsmetode som besvarer dem best.
| Kjernespørsmål | Kunnskap | Foretrukket studiedesign |
| Hvor mange har et helseproblem? | Prevalens – forekomst | Tverrsnittstudie |
| Hvorfor får noen dette problemet, mens andre holder seg friske? | Årsak – etiologi | Kohortstudie Kasus-kontrollstudie |
| Hvordan kan vi avgjøre om noen har dette problemet? | Diagnostikk | Tverrsnittstudie (med en referansestandard) |
| Hva kan vi gjøre for å forebygge eller behandle problemet? | Effekt av tiltak | Randomisert kontrollert studie (RCT) |
| Hvordan går det med den som har problemet? | Prognose – sykdomsforløp | Kohortstudie |
| Hvordan oppleves det? Hva er det som gjør at det virker? | Erfaringer og holdninger | Kvalitative metoder |
Lurer du på hva de ulike forskningsmetodene innebærer? Lillebeth Larun, Folkehelseinstituttet, gir en kort presentasjon av noen av de viktigste forskningsmetodene. (7:14 min):
3. Litteratursøk
Sist faglig oppdatert: 14.07.2017
Det tredje trinnet i kunnskapsbasert praksis er litteratursøk. Det innebærer å søke frem den beste tilgjengelige kunnskap.
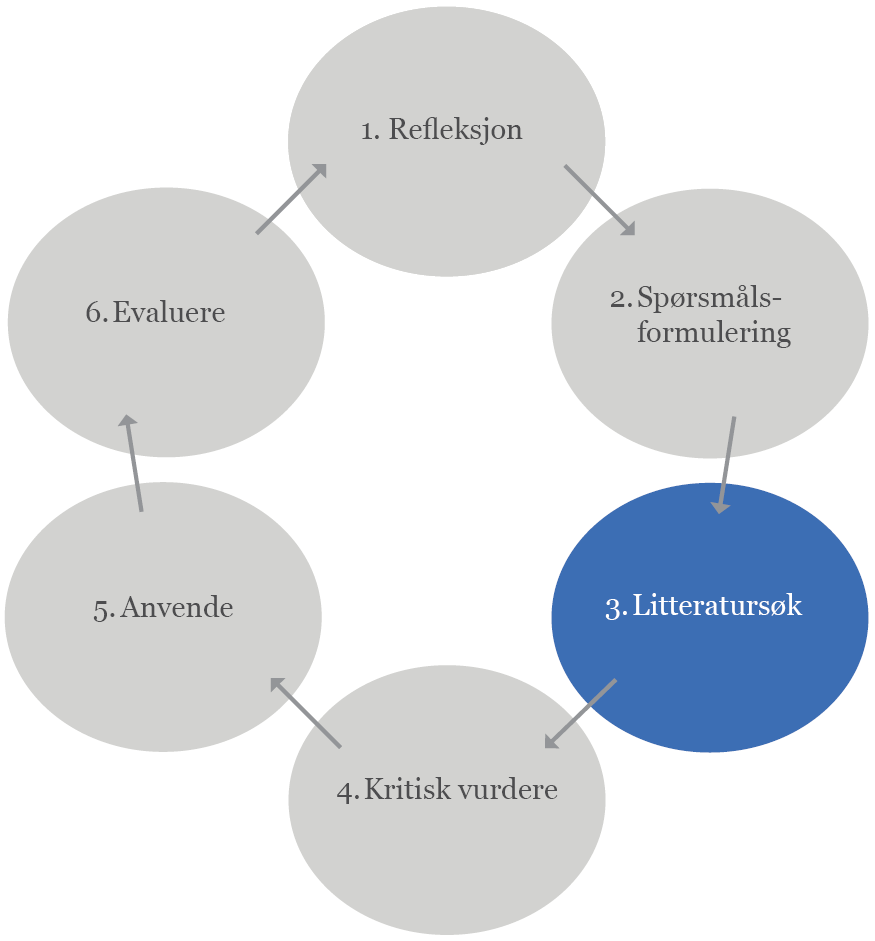
Når du skal finne den beste tilgjengelige kunnskap er ikke vanlige søkemotorer som Google, Bing o.l. særlig nyttige. Det er bedre å søke i spesielle kilder for forskningslitteratur. Slike kilder finner du mange av på Helsebiblioteket.no.
Hvilke kilder det er best å søke i avhenger av spørsmålet du skal finne svar på. Det er også viktig å finne de rette søkeordene og bruke søketeknikker tilpasset de kildene du søker i for å finne den beste kunnskapen. Klikk på lenkene i menyen til venstre for å lese mer om kildevalg, databaser, søkeord, emne- og tekstord, søketeknikker og det å lage søkestrategier.
3.1 Om Helsebiblioteket
Sist faglig oppdatert: 24.08.2017
Helsebiblioteket.no er et nasjonalt elektronisk bibliotek som kjøper inn en rekke databaser og kunnskapsressurser og gjør disse tilgjengelige via Helsebiblioteket.no. Dermed har helsepersonell i Norge gratis tilgang til viktige oppslagsverk, databaser og andre fagressurser.
Ressursene i Helsebiblioteket er en basispakke som er tilgjengelig for alt helsepersonell i Norge. De fleste fagbibliotekene ved utdanningsinstitusjoner og helseforetak abonnerer på en del ressurser i tillegg til det som finnes i Helsebiblioteket. Er du student eller ansatt i et helseforetak kan det derfor være best å gå via nettsidene til eget fagbibliotek når du skal søke.
3.2 Kildevalg
Sist faglig oppdatert: 28.08.2017
I Helsebiblioteket finner du mange databaser og kunnskapsressurser. Før du starter et søk er det lurt å tenke over:
1. Hva er spørsmålet mitt?
I trinn 2, spørsmålsformulering, presiserer vi problemstillingen og bestemmer type kjernespørsmål. Dette er viktig for å finne relevant forskningsbasert kunnskap effektivt. Du må for eksempel bruke andre kilder for å finne forskning på spørsmål om pasienterfaringer enn på spørsmål om effekt av tiltak.
2. Hva skal jeg lete etter?
Et viktig prinsipp i kunnskapsbasert praksis er å lete etter oppsummert forskning før du leter etter enkeltstudier. Oppsummert forskning kan være kvalitetsvurderte studier og systematiske oversikter. Det kan også være gode faglige retningslinjer der anbefalingene støtter seg på studier og oversikter som er systematisk samlet inn og kvalitetsvurdert.
Kunnskapspyramiden er en modell som hjelper deg å velge hva du skal søke etter og hvor du skal finne det. Kilder til oppsummert forskning ligger øverst i pyramiden og kilder til enkeltstudier ligger nederst. Start så høyt opp i pyramiden som mulig.
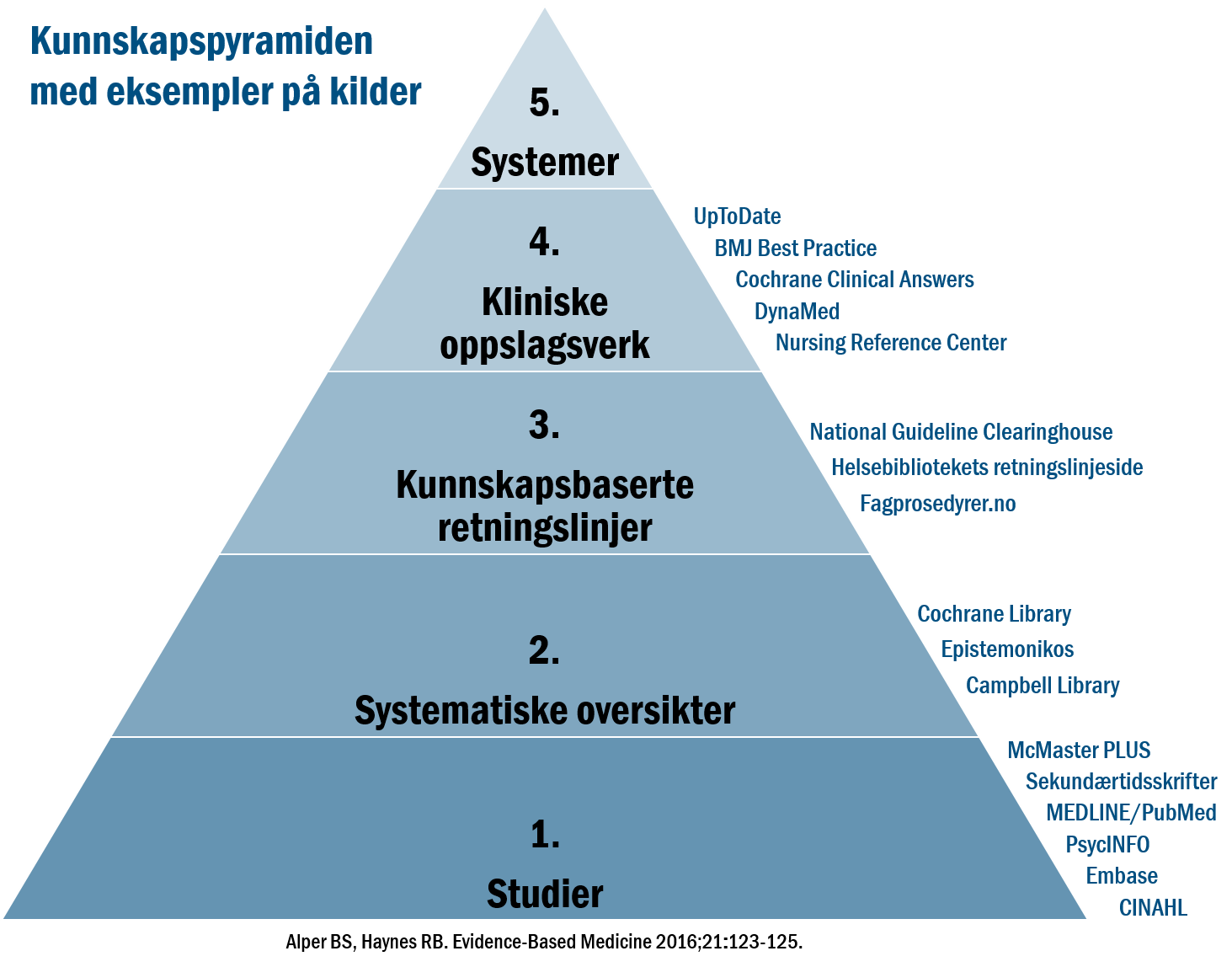
I denne videoen får du en kort innføring i Kunnskapspyramiden.
3.3 Databaser
Sist faglig oppdatert: 09.06.2017
Husk å søke etter oppsummert forskning først.
På Helsebiblioteket.no får du tilgang til de fleste databasene som er nevnt i denne nettressursen.
Her kan du også finne brukerveiledninger til databasene.
3.4 Søkeord
Sist faglig oppdatert: 31.08.2020
Emneord og tekstord
Vi skiller mellom to typer søkeord:
- Tekstord er ord i tittel og sammendrag, eller hele teksten i en artikkel (fulltekst). Et søk i Google er et tekstordsøk, vi skriver inn aktuelle ord i søkefeltet og får treff på nettsteder hvor ordene forekommer. Søk på tekstord kalles også fritekstsøk.
- Emneord er standardiserte ord som beskriver innholdet i artikler, bøker, og andre publikasjoner. Store databaser som MEDLINE og PsycINFO bruker standardiserte emneord. I MEDLINE heter emneordene MeSH, som står for Medical Subject Headings.
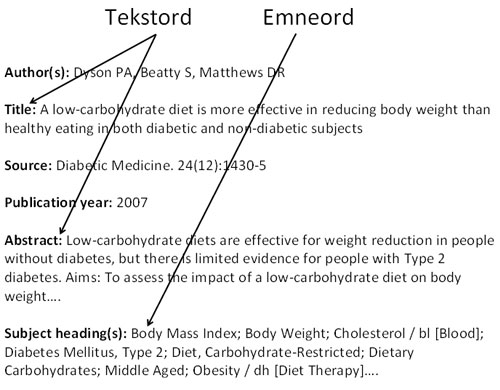
Ser du at artikkelen i eksemplet over har fått emneordet «Diet, Carbohydrate-Restricted» selv om forfatteren bruker «low carbohydrate diet»? Fordelen med standardiserte emneord er at du slipper å tenke på synonymer, ulike staveformer, og entalls-/flertallsendelser når du søker. Et søk på emneordet «Diet, Carbohydrate-Restricted» i MEDLINE gir treff på artikler om lavkarbohydratdietter uansett hvilke begreper forfatteren har brukt.
I databaser som MEDLINE, PsycINFO, Embase og CINAHL er det lurt å bruke faste emneord når du søker. Emneordene varierer mellom databasene, men har du funnet et relevant engelsk begrep hjelper databasen deg å finne det rette emneordet. I databaser som ikke bruker faste emneord, f.eks. Epistemonikos og deler av Cochrane Library må du søke med tekstord. Hvis du trenger å finne «alt» om et tema, er det lurt å søke på en kombinasjon av emne- og tekstord også i de basene som har et emneordssystem. Det er fordi det kan ta litt tid fra en artikkel kommer inn i databasen til den blir tildelt emneord og fordi indekseringen ikke alltid er helt presis.
Hvordan finne engelske søkeord?
Uansett om du skal søke med emneord eller tekstord må du finne engelske søkeord. Under er en del tips om hvor og hvordan du kan finne dem.
Artikler og bøker om temaet
Har du en artikkel eller bok på temaet fra før? Er artikkelen eller boka på engelsk vil du finne relevante ord i teksten. Er den på norsk kan du sjekke litteraturlisten, forfattere refererer ofte til engelskspråklig litteratur om temaet. Det kan også være smart å søke opp artikkelen i databaser som MEDLINE, Embase og CINAHL for å se hvilke emneord den har fått der.
Ordbøker og oppslagsverk
Wikipedia - Tips: Søk på det norske begrepet, og velg English under andre språk i venstre meny.
Merriam-Webster Medical Dictionary
SveMed+
Alle referanser i SveMed+ får engelske MeSH-emneord uansett om artiklene er skrevet på svensk, norsk, dansk eller engelsk. Alle titler blir også oversatt til engelsk. Du kan derfor søke på norsk, svensk eller dansk i SveMed+ og lete etter engelske søkeord i emneordene og de oversatte titlene. Veiledning for å finne engelske søkeord i SveMed+ (PDF, 433 KB).
MeSH på norsk og engelsk
Deler av MeSH er oversatt til norsk. I databasen MeSH på norsk og engelsk kan du søke på norsk og finne tilsvarende engelsk MeSH. MERK: MeSH på norsk og engelsk er ikke oppdatert siden 2017.
Helsebiblioteket
På helsebiblioteket.no kan du enkelt søke i en rekke kilder. Søket ditt oversettes automatisk til/fra engelsk og synonymer er også inkludert. Derfor kan dette være et godt utgangspunkt for å finne relevante søkeord.
3.5 Søketeknikker
Sist faglig oppdatert: 27.11.2020
Ulike databaser krever ulike måter å søke på. Derfor må du gjøre deg kjent med søketeknikken til den eller de basene du skal søke i.
Kombinere søkeord
Når du har funnet relevante søkeord må du kombinere dem på riktig måte i databasen ved å bruke kombinasjonsord (boolske operatorer). De vanligste kombinasjonsordene er AND, OR og NOT.
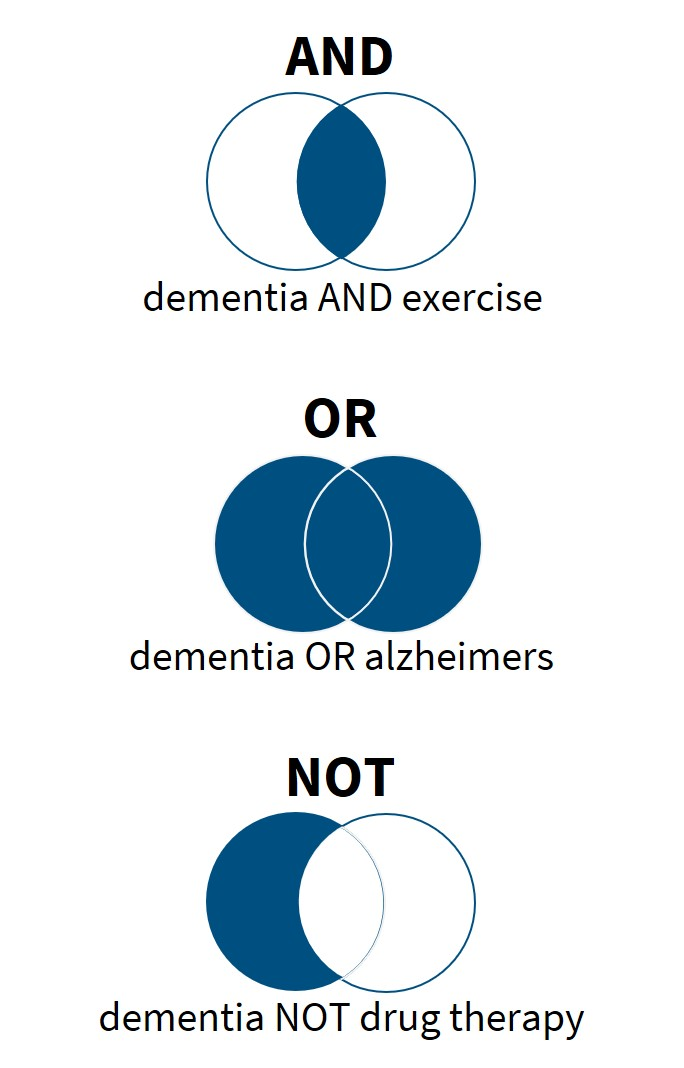
AND avgrenser søket fordi begge søkeordene må være med i artikkelreferansen: dementia AND exercise.
OR utvider søket ved å gi treff på artikkelreferanser som inneholder enten det ene, det andre eller begge søkeordene: dementia OR alzheimers.
NOT avgrenser søket fordi kun det ene, ikke det andre søkeordet, skal være med i artikkelreferansen:
dementia NOT drug therapy. Viktig: NOT må brukes med stor forsiktighet for du risikerer å ekskludere relevante treff ved bruk av NOT.
Vilde Farup Halvorsen fra OsloMet forklarer boolske operatorer (2:39)
Trunkering
Trunkering brukes når du søker på tekstord. Å trunkere betyr å søke på stammen av et ord for å få med entalls-/flertallsendelser og ulike varianter av ordet. Svært ofte er trunkeringstegnet en stjerne (*). Et søk på vaccin* gir treff på vaccine, vaccines, vaccination, vaccinating osv.
Vilde Farup Halvorsen fra OsloMet forklarer trunkering (1:00)
3.6 Lage søkestrategi
Sist faglig oppdatert: 15.11.2020
Nå skal vi se på hvordan du med utgangspunkt i et PICO-skjema med emne- og tekstord kan lage søkestrategier.
| Norske ord | MeSH (emneord) | Tekstord | |
| Population/ Problem | Overvekt | Overweight | Overweight Obesity |
| Intervention | Lavkarbodiett | Diet, Carbohydrate-Restricted | Carbohydrate restricted diet(s) Low carbohydrate diet(s) |
| Comparator | Fettfattig diett | Diet, Fat-Restricted | Fat-restricted diet(s) Low-fat diet(s) Fat-free diet(s) |
| Outcome | Vektreduksjon | Weight loss | Weight loss(es) Weight reduction(s) |
Hvordan kombinerer jeg søkeordene?
Hver linje i PICO-tabellen (populasjon, intervensjon osv.) kaller vi et PICO-element. I eksempelet over er alle PICO-elementene tatt med. Ofte trenger du bare å søke på et par av elementene, f.eks. populasjon og intervensjon. Legg heller til flere elementer (for eksempel utfall) hvis du får for mange treff. Husk også at ikke alle spørsmål har alle PICO-elementene i seg.
Huskeregel: kombiner alle ordene innenfor hvert enkelt PICO-element med OR og til slutt alle PICO-elementene med AND.
| P | 1. overweight 2. obesity 3. Overweight/ (MeSH) |
|---|---|
| I | 5. carbohydrate restricted diet* 6. low carbohydrate diet* 7. Diet, Carbohydrate-Restricted/ (MeSH) |
| C | 9. fat restricted diet* 10. low fat diet* 11. fat free diet* 12. Diet, Fat- Restricted/ (MeSH) |
| O | 14. weight loss* 15. weight reduction* 16. Weight loss/ (MeSH) |
PICO | 18. 4 AND 8 AND 13 AND 17 |
I dette eksempelet har vi søkt på både tekstord (ord i tittel/sammendrag) og standardiserte emneord (MeSH). Du kan velge å kun søke på emneord eller kun på tekstord, men hvis du skal gjøre et grundig systematisk søk, anbefaler vi å bruke begge deler.
Noen databaser inneholder ikke standardiserte emneord. Da må du søke på tekstord og huske å få med synonymer og ulike staveformer.
Hvordan utfører jeg søket i praksis?
Søk på ett begrep av gangen. Når du har søkt på alle begrepene i et PICO-element, gå til søkehistorikken («search history») og kombiner med OR. Helt til sist kombinerer du alle PICO-elementene med AND (som illustrert i tabellen ovenfor). Måten man setter opp søk på varierer mye mellom ulike databaser. På Helsebiblioteket.no kan du finne veiledninger for søk i mange ulike databaser.
Begrense søket til forskningsmetode og/eller kjernespørsmål
I noen databaser, for eksempel i Cochrane Library, sorteres søkeresultatet automatisk etter forskningsmetode (systematiske oversikter og randomiserte kontrollerte studier). I andre databaser, slik som MEDLINE (Ovid), Embase (Ovid) og CINAHL (EBSCO) må du selv definere om du vil avgrense søket til en eller flere typer forskningsmetode.
Når du har gjort et søk i MEDLINE eller Embase fra Ovid, se etter funksjonen «Limits» og «Additional Limits». Der kan du bruke «Clinical Queries» til å avgrense søkeresultatet til det kjernespørsmålet du ønsker å få svar på, f.eks. «therapy», «diagnosis» eller «prognosis». I CINAHL (EBSCO) klikker du på «Edit» i søkehistorikken for å finne «Clinical Queries».
I PubMed kan du gå direkte til funksjonen «Clinical Queries» under «Find» på startsiden. Der kan du velge kategorier som f.eks. «therapy», «diagnosis» eller «prognosis».
4. Kritisk vurdering
Sist faglig oppdatert: 11.12.2018
Forskningsresultater kan ikke brukes ukritisk. Hensikten med kritisk vurdering (trinn 4) er å vurdere gyldigheten av informasjonen i studien. Det er viktig at den metodiske kvaliteten og konteksten studien er gjennomført i blir vurdert.
Hvorfor vurdere?
Denne delen er en innføring i hvordan du kritisk vurderer den metodiske kvaliteten i forskningsartikler. Du lurer kanskje på hvorfor det er nødvendig å vurdere artikler som er publisert i vitenskapelige tidsskrifter? Selv om artikler er publisert i velrenommerte tidsskrifter, er det likevel viktig å vurdere artikkelens gyldighet, metodiske kvalitet, resultater og overførbarhet.
Tabellen med kjernespørsmål, hvilken type kunnskap disse gir og hvilken forskningsmetode som er best egnet, er et godt utgangspunkt når du skal kritisk vurdere artikler. I tillegg til at kritisk vurdering sier noe om hvor god artikkelen er, kan du også bruke den for å lære mer om forskningsmetode.
| Kjernespørsmål | Kunnskap | Foretrukket studiedesign |
| Hvor mange har et helseproblem? | Prevalens – forekomst | Tverrsnittstudie |
| Hvorfor får noen dette problemet, mens andre holder seg friske? | Årsak – etiologi | Kohortstudie Kasus-kontrollstudie |
| Hvordan kan vi avgjøre om noen har dette problemet? | Diagnostikk | Tverrsnittstudie (med en referansestandard) |
| Hva kan vi gjøre for å forebygge eller behandle problemet? | Effekt av tiltak | Randomisert kontrollert studie (RCT) |
| Hvordan går det med den som har problemet? | Prognose – sykdomsforløp | Kohortstudie |
| Hvordan oppleves det? Hva er det som gjør at det virker? | Erfaringer og holdninger | Kvalitative metoder |
Sjekklister
Det er utarbeidet sjekklister som gjør det lettere å kritisk vurdere den metodiske kvaliteten i vitenskapelige artikler. Ulike spørsmål krever ulike forskningsmetoder, og du må derfor bruke sjekklister som passer forskningsmetoden i den enkelte artikkelen.
Statistikk
Statistikk er viktig for å forstå resultatene i en artikkel, men mange har et anstrengt forhold til tall og statistikk. Under 4.8 Statistikk i menyen til venstre finner du lenker til sider som på en enkel måte og ved hjelp av konkrete eksempler gir en innføring i statistikk. Vi anbefaler også artikkelen Brurberg KG, Hammer H. Hvorfor trenger vi statistikk?. Sykepleien Forskn. 2013;8(1):78-82.
4.1 Sjekklister
Sist faglig oppdatert: 17.09.2021
Det finnes ulike sjekklister for ulike typer studiedesign, men sjekklistene har noen fellestrekk. Du bør stille to overordnede spørsmål som første ledd i kritisk vurdering:
- Har artikkelen en klart formulert problemstilling?
- Er designet velegnet for å svare på problemstillingen?
Dersom du svarer «nei» på ett av disse, bør du allerede vurdere å legge fra deg artikkelen.
De neste spørsmålene du bør stille deg:
- Kan du stole på resultatene?
- Hva er resultatene?
- Kan resultatene brukes i min praksis?
Dette er generelle overordnede spørsmål som bør stilles uavhengig av forskningsmetode. I tillegg anbefaler vi at du går grundig igjennom sjekklisten som passer forskningsmetoden i artikkelen du skal vurdere.
Sjekklister for å lære og øve på kritisk vurdering
Sjekklistene nedenfor er laget som pedagogiske verktøy for å lære kritisk vurdering av vitenskapelige artikler. Vi jobber for tiden med å få sjekklistene over i universell utforming og derfor har sjekklistene forskjellig layout. Sjekklistene kan fylles ut elektronisk, dette gjelder også sjekklistene i PDF-format der man kan krysse av i boksene og klikke i feltet under for å fylle inn kommentarer.
Oversiktsartikkel (Word, 35 kB)
Eksempel: Tiltak ved korsryggsmerter (PDF 311 kB)
Randomisert kontrollert studie (Word, 34 kB)
Eksempel: Ikke-invasiv ventilasjonsbehandling ved kols (PDF 230 kB)
Kvalitativ studie (Word, 35 kB)
Prevalensstudie (PDF, 61 KB) Under revidering, vurder å bruke engelskspråklig sjekkliste fra JBI: Checklist for Prevalence Studies
Tverrsnittstudie - norsk versjon kommer, bruk eventuelt engelskspråklig sjekkliste fra JBI: Checklist for Analytical Cross Sectional Studies
Diagnosestudie (Skrivbar PDF, 5 MB)
Kohortstudie (Skrivbar PDF, 5 MB)
Kasuskontrollstudie (Skrivbar PDF, 5 MB)
Innendeltakerdesign (single-case experimental design) (Word, 46kB)
Retningslinje eller fagprosedyre (Word, 39 kB)
Eksempel: Remdesivir ved covid-19 (PDF 296 kB)
Kapitler i kliniske oppslagsverk (Word, 32 kB)
Eksempel: Alternativ supplerende kommunikasjon ved autisme (PDF 236 kB)
Sjekklister for kritisk vurdering på engelsk og flere andre språk er tilgjengelige fra Centre for Evidence Based Medicine ved University of Oxford, fra Critical Appraisal Skills Programme (CASP) ved Better Value Healthcare i Oxford og fra JBI som er en del av Faculty of Health and Medical Sciences ved University of Adelaide.
Sjekklister for kritisk vurdering til bruk i systematiske oversikter eller forskningsprosjekter
Hvis du skal kritisk vurdere artikler til bruk i en systematisk oversikt eller andre forskningsprosjekter bør du bruke mer omfattende sjekklister, som for eksempel:
- For randomiserte kontrollerte studier Cochrane Risk of Bias 2 (RoB 2) tool
- For ikke-randomiserte studier av intervensjoner: ROBINS-I tool
- For ikke-randomiserte studer av eksponeringer: ROBINS-E tool
- For diagnosestudier: QUADAS-2 tool
- For systematiske oversikter ROBIS
Har du kommentarer eller forslag til andre sjekklister som bør være med på denne siden? Send e-post til redaktøren.
4.2 Systematisk oversikt
Sist faglig oppdatert: 01.09.2022
En systematisk oversikt, eller systematisk kunnskapsoppsummering, er en oversikt over flere artikler om samme emne. Det er viktig at det er brukt en systematisk og beskrevet fremgangsmåte for å finne, vurdere og oppsummere enkeltstudiene.
I denne delen finner du videoer om hva systematiske oversikter er, hvordan du kritisk vurderer den metodiske kvaliteten og hvordan du kan vurdere av tillit til resultatene med GRADE.
Tidligere Nasjonalt kunnskapssenter for helsetjenesten (nå innlemmet i Folkehelseinstituttet) har laget denne videoen om hva systematiske oversikter er og hvordan de lages (3:23):
Systematisk oversikt eller systematisk kunnskapsoppsummering kalles på engelsk systematic review eller eller evidence syntehsis. Denne videoen fra Evidence Synthesis Ireland og Cochrane Ireland gir en enkel fremstilling av hva "evidence synthesis" er (3:29):
En god systematisk oversikt gir leseren oversikt over hva som finnes om et bestemt emne, og om kvaliteten på forskningen.
Systematiske oversikter gjør kunnskapen lettere tilgjengelig.
Samling av studier om en problemstilling
Formålet med systematiske oversikter er å se forskningsresultater fra relevante studier om en problemstilling under ett. En systematisk oversikt gir et balansert bilde av hva forskning har vist om en bestemt problemstilling.
I prinsippet kan systematiske oversikter sammenstille studier av alle typer forskningsmetoder og for alle kjernespørsmål. Systematiske oversikter blir oftest brukt i vurdering av effektspørsmål, men det finnes også systematiske oversikter for andre forskningsmetoder (f.eks diagnosestudier eller kvalitative studier).
En god systematisk oversikt kjennetegnes ved at den har:
- En klar tittel og klart formål
- En omfattende og beskrevet søkestrategi
- Klare kriterier for inklusjon og eksklusjon av primærstudier
- Vurdering av kvalitet på inkluderte studier
- Beskrivelse av karakteristiske trekk for alle inkluderte studier
Sammenstilling av resultatene fra inkluderte studier kan bestå av en beskrivende oppsummering, eller være en eller flere meta-analyser. Resultatene fra de enkelte studiene er analysert sammen for å gi et samlet resultat for flere eller alle studiene.
Kritisk vurdering av systematiske oversikter
- Er formålet med oversikten klart formulert?
- Er det klare kriterier for inklusjon av enkeltstudiene?
- Er det sannsynlig at relevante studier er funnet?
- Er kvaliteten på de inkluderte studiene vurdert?
- Dersom resultatene fra de inkluderte studiene er kombinert statistisk i en meta-analyse, var dette fornuftig og forsvarlig?
- Dersom det ikke er gjennomført en meta-analyse – er dette valget begrunnet?
- Hvor presise er resultatene?
- Kan resultatene overføres til praksis?
Bente Frisk og Nina Rydland Olsen, Høgskulen på Vestlandet viser i denne videoen hvordan man kan bruke sjekkliste for oversiktsartikler til kritisk vurdering av en systematisk oversikt1 (8:45).
Vurdering av tillit til resultatene i en systematisk oversikt
Når forfatterne av en systematisk oversikt har en eller flere relevante studier som har informasjon om en bestemt sammenligning og et eller flere utfall (f.eks. om effekten av et bestemt tiltak mot smerte sammenliknet med et annet tiltak eller ikke noe tiltak), bør de vurdere hvilken tillit de har til resultatene. Er det grunn til å tro at dette samlet sett er et robust effektestimat, som neppe vil bli påvirket selv om det kommer nye studier? GRADE (Grading of Recommendations Assessment, Development and Evaluation) brukes for å vurdere tilliten til resultatene i en systematisk oversikt og styrken anbefalingene i en retningslinje2.
Per Olav Vandvik, Universitetet i Oslo og Lovisenberg diakonale sykehus, forteller i denne videoen hvordan GRADE kan brukes, i tillegg til sjekklister, til kritisk vurdering av systematiske oversikter (6:53).
- van Middelkoop, M., Rubinstein, S. M., Kuijpers, T., Verhagen, A. P., Ostelo, R., Koes, B. W., & van Tulder, M. W. (2011). A systematic review on the effectiveness of physical and rehabilitation interventions for chronic non-specific low back pain. European spine journal : official publication of the European Spine Society, the European Spinal Deformity Society, and the European Section of the Cervical Spine Research Society, 20(1), 19–39.
- Folkehelseintituttet. (2022, 22. april). Slik oppsummerer vi forsking. Hente ut data, sammenfatte og gradere. Folkehelseinstituttet.
4.3 Randomisert kontrollert studie
Sist faglig oppdatert: 14.05.2019
Dersom spørsmålet ditt handler om effekt av et tiltak, er randomisert kontrollert studie (randomised controlled trial, RCT) den beste forskningsmetoden. RCT er en metode der vanligvis to grupper sammenlignes. Gruppene som skal sammenlignes bør være så like som mulig med hensyn til alt som kan påvirke utfallet. Dette oppnår man ved å tilfeldig fordele (randomisere).
| Kjernespørsmål | Kunnskap | Foretrukket studiedesign |
| Hva kan vi gjøre for å forebygge eller behandle problemet? | Effekt av tiltak | Randomisert kontrollert studie |
I en randomisert kontrollert studie skal deltagerne fordeles tilfeldig i tiltaksgruppe og kontrollgruppe. Når et nytt tiltak, f.eks. et medikament, skal testes ut, randomiserer man deltagerne i to grupper. Den ene gruppen får medikamentet (tiltaksgruppe eller intervensjonsgruppe), mens den andre gruppen (kontrollgruppen) ikke får medikamentet.
Randomisering er teknikken som med størst sannsynlighet gir sammenlignbare grupper.
Tilfeldig fordeling får vi (i prinsippet) ved å slå mynt og krone (i praksis ved å la et dataprogram gjøre arbeidet).
En randomisert kontrollert studie foregår over en tidsperiode. Etter en gitt tidsperiode sammenlignes de to gruppene, og sammenligningen viser om medikamentet har effekt eller ikke.
Kritisk vurdering av RCT:
-
Er fomålet med studien klart formulert?
-
Er en randomisert kontrollert studie et velegnet design for å besvare spørsmålet?
-
Kan du stole på resultatene?
-
Hva er resultatene?
-
Kan resultatene brukes i min praksis?
I denne forelesningen av Hildegunn Lygren, Høgskolen i Bergen, får du en presentasjon av hva en randomisert kontrollert studie er, og eksempler på problemstillinger der RCT er det riktige studiedesign å bruke (7:54 min).
I denne videoen viser Liv Heide Magnussen og Vegard Pihl Moen ved Høgskulen på Vestlandet hvordan du kan kritisk vurdere en randomisert kontrollert studie1 ved hjelp av sjekkliste for RCT (8:50 min).
- Andersen, L. N., Juul-Kristensen, B., Sørensen, T. L., Herborg, L. G., Roessler, K. K., & Søgaard, K. (2016). Longer term follow-up on effects of Tailored Physical Activity or Chronic Pain Self-Management Programme on return-to-work: A randomized controlled trial. Journal of rehabilitation medicine, 48(10), 887–892.
4.4 Kvalitativ metode
Sist faglig oppdatert: 31.08.2022
Kvalitativ forskningsmetode brukes for å undersøke og beskrive menneskers opplevelse og erfaringer. Det finnes forskjellige måter å fremskaffe denne kunnskapen på. Kvalitativ metode er en fleksibel forskningsmetode, og det kan være utfordrende å sette seg inn i metoden.
| Kjernespørsmål | Kunnskap | Foretrukket studiedesign |
Hvordan oppleves det? | Erfaringer og holdninger | Kvalitative metoder |
Datainnsamling og analyse
Datainnsamling skjer hovedsakelig gjennom intervju eller observasjon, men kan også ha andre former. For å oppnå et rikt beskrivende datamateriale, har man et relativt lite utvalg deltagere i kvalitativ forskning.
Analyse av kvalitative data kan variere, avhengig av den retningen man arbeider innenfor. Gjennom analyse prøver forskerne å finne mening i datamaterialet. Funnene presenteres i et beskrivende og fortellende format, med utdrag fra datamaterialet for å underbygge og illustrere hovedtemaene.
Kritisk vurdering av kvalitative studier
Det er debatt om hvorvidt én standardisert sjekkliste kan benyttes på alle typer kvalitative studier. En sjekkliste vil aldri kunne dekke alle sider av artikler, men er ment å hjelpe deg når du skal vurdere om artikkelen har bruksverdi i din praksis.
Sjekklisten dekker følgende områder:
Har artikkelen en klart formulert problemstilling?
- I en god artikkel bør du finne et klart og tydelig formål på slutten av introduksjonen. I tillegg bør formålet være presentert i abstractet (sammendraget). Sammenfaller artikkelens problemstilling med ditt spørsmål? Hvis du ser at den ikke gjør det, må du kanskje legge artikkelen til side og se om du finner en som er mer relevant.
Er metoden som er benyttet velegnet for å besvare problemstillingen?
- For å finne ut av dette, kan du bruke tabellen over som hjelpemiddel. Dersom du vet at du ønsker kunnskap om personers opplevelse og erfaring, ser du i tabellen at foretrukket forskningsmetode er kvalitativ metode.
Kan du stole på resultatene?
- Svaret på dette finner du som oftest i metodedelen i artikkelen. Her må du stille deg kritisk til utvalget, datainnsamlingen og analysemetoden som er brukt i studien.
Hva er resultatene?
- De sentrale hovedfunnene i studien skal komme klart frem i artikkelen.
Kan resultatene brukes i min praksis?
Janet Harris, Høgskolen i Bergen, gir deg en presentasjon av kvalitativ forskningsmetode, og en måte å kritisk vurdere kvalitative artikler på (10:13 min).
I denne videoen viser Tove Ask og Liv Heide Magnussen ved Høgskulen på Vestlandet hvordan du kan kritisk vurdere en kvalitativ studie1 ved hjelp av sjekkliste for kvalitative studier (9:38 min).
- Coole, C., Drummond, A., Watson, P. J., & Radford, K. (2010). What concerns workers with low back pain? Findings of a qualitative study of patients referred for rehabilitation. Journal of occupational rehabilitation, 20(4), 472–480.
4.5 Tverrsnittstudie
Sist faglig oppdatert: 16.06.2017
Metoden brukes mest når en skal beskrive forekomst (prevalens), f.eks. fysisk aktivitet, men kan også utforske sammenhenger, f.eks. mellom fysisk aktivitet og kosthold.
En standard tverrsnittundersøkelse kan ikke si noe sikkert om årsaksforhold. De fleste markedsundersøkelser er tverrsnittstudier.
| Kjernespørsmål | Kunnskap | Foretrukket studiedesign |
| Hvor mange har et helseproblem? | Prevalens – forekomst | Tverrsnittsstudie |
Kritisk vurdering av tverrsnittstudier:
- Er problemstillingen klart formulert?
- Er befolkningen (populasjonen) som utvalget er tatt fra, klart definert?
- Ble utvalget inkludert i studien på en tilfredsstillende måte?
- Ble det redegjort for om respondentene skiller seg fra de som ikke har respondert?
- Er svarprosenten høy nok?
- Bruker studien målemetoder som er pålitelige for det som skal måles?
- Er datainnsamlingen standardisert?
- Er dataanalysen standardisert?
- Hva forteller resultatene?
- Kan det overføres til praksis?
Monica W. Nortvedt, Høgskolen i Bergen, presenterer tverrsnittstudie. Monica er leder for Senter for kunnskapsbasert praksis, HiB. Hun underviser i KBP og har skrevet lærebok om emnet.
4.6 Diagnostiske tester
Sist faglig oppdatert: 14.05.2019
For å vurdere om en test er god må den sammenlignes med en referansetest (den beste testen som finnes på området). Et eksempel kan være om hvisketest er en pålitelig test for å avdekke hørselsproblemer hos eldre hvor referansetesten er audiometri.
| Kjernespørsmål | Kunnskap | Foretrukket studiedesign |
| Hvordan kan vi avgjøre om noen har dette problemet? | Diagnostikk | Tverrsnittsstudie (med en referansestandard) |
Kritisk vurdering av diagnostiske tester:
- Er formålet med studien klart formulert?
- Ble det utført en sammenligning med en egnet referansetest?
- Fikk alle pasientene/individene den diagnostiske testen og referansetesten?
- Kan resultatene på referansetesten ha hatt innflytelse på testen som vurderes?
- Er sykdomsstatusen på populasjonen som testes, klart beskrevet?
- Ble metodene for utførelsen av testen godt nok beskrevet?
- Hva forteller resultatene?
- Kan det overføres til praksis?
I denne forelesningen av Per Vandvik, Kunnskapssenteret, får du en presentasjon av hva en diagnostisk studie er, og eksempler på problemstillinger der diagnostiske tester er den riktige forskningsmetoden å bruke.
Ønsker du å trene på kritisk vurdering av diagnostiske tester? Her finner du en artikkel og sjekkliste for diagnostiske tester.
4.7 Faglige retningslinjer
Sist faglig oppdatert: 15.12.2020
Retningslinjer er anbefalinger for praksis som skal gi beslutningsstøtte og være basert på beste tilgjengelige kunnskap. En mye brukt definisjon er:
”… systematisk utviklede råd og konklusjoner for å hjelpe helsearbeider og pasient til å velge å passende/hensiktsmessig behandling for en definert klinisk problemstilling”.1
En kunnskapsbasert retningslinje (eller for eksempel veileder, prosedyre, handlingsprogram) betyr at beslutningsgrunnlaget som sier hvilke tiltak som skal iverksettes er basert på vitenskapelig dokumentasjon som er systematisk samlet inn. Denne vitenskapelige dokumentasjonen skal også være kritisk vurdert. Her bruker vi metoder som er lik de som brukes i arbeidet med systematiske oversikter. Men å gi anbefalinger for praksis, betyr også at dokumentasjonen vurderes i forhold til aktuelle praksisfelt. Det skal blant annet tas hensyn til ressurser, hva som er akseptabelt for pasienter, hva som er akseptabelt for helsearbeider, økonomi og etikk.
Gode retningslinjer kan endre praksis og føre til bedre helse hos pasientene. Hvordan helsepersonell bruker retningslinjene for å utvikle, iverksette og følge opp påvirker i hvilken grad de blir brukt. Å iverksette tiltakene fordrer at den enkelte helsearbeider også bruker sitt faglige skjønn selv om anbefalingene i utgangspunktet er basert på den beste tilgjengelige forskningsbaserte kunnskap.
Tilgjengelige retningslinjer (veiledere, prosedyrer og handlingsprogram) er av ulik kvalitet. Det er derfor utviklet verktøy som hjelper deg å vurdere om du kan stole på anbefalingene som gis eller ikke. Et internasjonalt anerkjent og utprøvd verktøy for å vurdere retningslinjer er AGREE. Når vi vurderer faglige retningslinjer i denne sammenheng har vi valgt å presentere et litt mindre strengt verktøy som er enklere å bruke i praksis.
1Hayward, R. S., Wilson, M. C., Tunis, S. R., Bass, E. B., & Guyatt, G. (1995). Users' guides to the medical literature. VIII. How to use clinical practice guidelines. A. Are the recommendations valid? The Evidence-Based Medicine Working Group. JAMA, 274(7), 570–574.
Kritisk vurdering av faglige retningslinjer:
- Kommer det klart fram hva retningslinjen handler om og hvem som er målgruppen?
- Er det gjort rede for hvem som har utarbeidet retningslinjen?
- Er det forskningsbaserte dokumentasjonsgrunnlaget innhentet på en tilfredsstillende måte?
- Er den metodiske kvaliteten til inkluderte studier vurdert og er det beskrevet hvilke kriterier man har benyttet?
- Er retningslinjene basert på oppdatert kunnskap?
- Er dokumentasjonsgrunnlaget for retningslinjen tydelig vurdert og gradert
- Hva forteller retningslinjene?
- Kan retningslinjene være til hjelp i praksis?
Vil du øve på kritisk vurdering av faglige retningslinjer? Bruk sjekkliste for kritisk vurdering av faglige retningslinjer og fagprosedyrer. Retningslinjer kan du f.eks. finne via Helsebibliotekets retningslinjesider eller hos RNAO.
Her finner du eksempel på utfylt sjekkliste for kritisk vurdering av en faglig retningslinje om remdesivir ved covid-19.
Liv Merete Reinar, Kunnskapssenteret, gir i denne videoen en enkel innføring i hva en faglig retningslinje er og hvordan man kan kritisk vurdere dem.
4.8 Statistikk
Sist faglig oppdatert: 11.06.2017
Her finner du lenker til sider som på en enkel måte og ved hjelp av konkrete eksempler gir en innføring i statistikk.
Hvis du lurer på hvor mange nordmenn som er motstandere av røykeloven kan du gjøre en spørreundersøkelse. Hvis du lurer på om det en noen vits i å slutte å røyke kan du sammenligne levetid blant røykere og ikke-røykere. Hvis du lurer på om nikotintyggegummi bidrar til enklere røykeavvenning finner du svaret i randomiserte kontrollert studier. Hvilken fremgangsmåte du bruker for å finne svar vil variere, men uansett spørsmål vil svaret nesten alltid være knyttet opp mot et eller flere tall.
Tall er vanligvis viktig for å forstå resultatene i en artikkel. Her forsøker vi å forklare tallenes tale på en enkel måte og ved hjelp av konkrete eksempler.
4.8.1 Beskrive tall
Sist faglig oppdatert: 24.08.2022
Statistikk er å analysere og beskrive ved hjelp av tall. Tallene kan beskrive hvor mange (som er syke), hvor ofte (opptrer symptomer) og hvor mye (alvorlighetsgrad).
Populasjon og utvalg
Det finnes eksempler der statistikk baserer seg på hele den aktuelle befolkningen eller populasjonen, for eksempel medisinsk fødselsregister. For mange formål er det upraktisk å samle statistikk om hele populasjonen.
Et av hovedformålene med bruk av statistikk er å trekke slutninger om en populasjon basert på et mindre utvalg.
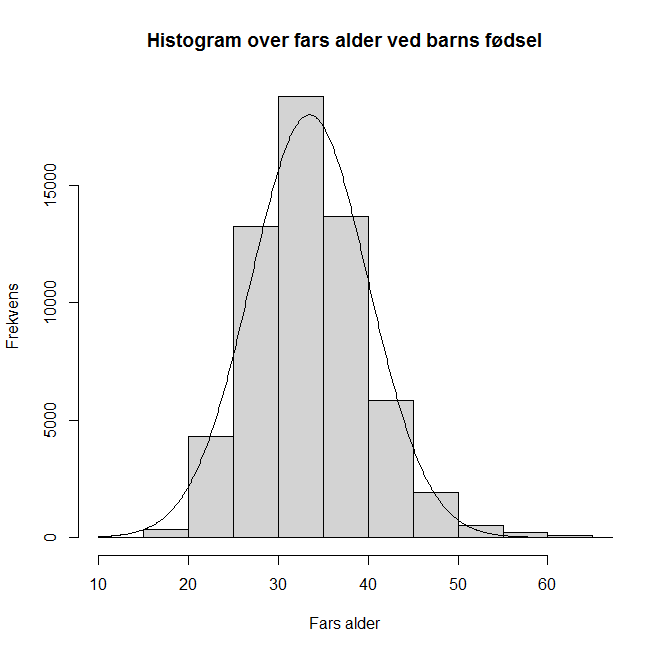
Tabell 1 – Histogram over fars alder ved barns fødsel
Histogrammet over viser alle registrerte fødsler i 2011 og hvordan nybakte fedre fordeler seg i ulike alderskategorier (Figur 1). Noen av de som ble fedre i 2011 var yngre enn 20 år og noen var eldre enn 50 år, men de fleste var mellom 30 og 35 år. Hyppigheten (frekvensen) viser hvor mange som er i hver kategori, f.eks. er 18784 nybakte fedre (32 %) mellom 30 og 35 år.
Når vi måler alder på et stort antall mennesker vil resultatene fordele seg i en normalkurve. Normalkurven viser sentraltendens og spredning ved hjelp av gjennomsnitt (M) og standardavvik (SD). Gjennomsnittlig alder for de som ble fedre i 2011 er 33 år og standardavviket er 6.5. I eksempelet er det benyttet 11 alderskategorier à 5 år (søylebredder) og histogrammet antar en tilnærmet klokkeform (linje).
I statistikken ser vi ofte histogram med en slik klokkeform, og vi sier da at data følger en Gauss- eller normalfordelingskurve.
Normalfordelingskurven er symmetrisk, det vil si at kurven er like bratt enten man beveger seg fra midten mot venstre eller fra midten mot høyre. Slike symmetriske data dukker ofte opp i reelle situasjoner, men i den virkelige verden finnes det mange eksempler på data som ikke er normalfordelt (klokkeformet).
Figur 2 oppsummerer norske arbeidsledighetstall fra 2012 og illustrerer skjevfordelte data som ikke passer med normalfordelingen. Når fordelingen er skjev (ikke normalfordelt) brukes vanligvis median som sentraltendens og spredning vises med interkvartil bredde (inter quartile range) eller prosentiler (percentiles). I figur 2 er medianen 10 uker, 25 % prosentilen 4 uker, 75 % prosentilen 38 uker og interkvartil bredde er 34 uker.
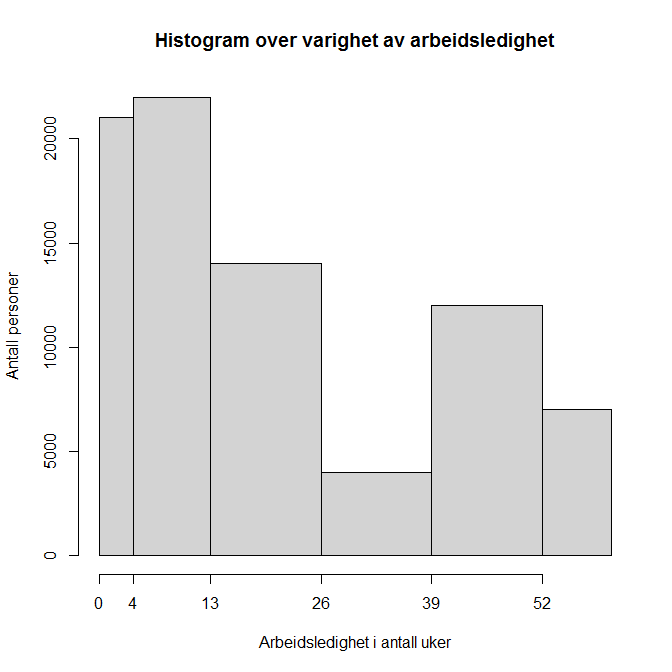
Figur 2 – Histogram over varighet av arbeidsledighet
I denne videoen laget for KBP på tvers ved Høgskulen på Vestlandet får du en enkel innføring i deskriptiv statistikk (3:42 min)
Eva Denison, Kunnskapssenteret, gir en innføring i hvordan du kan beskrive tall. Eva underviser i statistikk og kunnskapsbasert praksis for helsepersonell. I tillegg skriver hun kunnskapsoppsummeringer m.m. og har skrevet bruksanvisninger for ulike statistikkprogram (9:30 min).
4.8.2 Analysere tall
Sist faglig oppdatert: 24.08.2022
For å kunne stole på resultatene må vi være rimelig sikre på at det verken er systematiske eller tilfeldige feil i studien. En kritisk vurdering av hvordan forskerne gikk fram gir oss svar på om det kan foreligge systematiske feil, mens faget statistikk hjelper oss å vurdere om resultatene kan skyldes tilfeldige feil. Det kan vi bedømme ved å utnytte hjelpemidler som konfidensintervall eller statistiske tester. Statistikken hjelper oss å reflektere om hva som ville ha skjedd dersom den aktuelle studien var blitt gjentatt mange ganger. Dermed kan vi få en formening om det er rimelig å anta at resultatene ikke bare gjelder for dem som ble undersøkt i akkurat denne studien, men også for alle andre liknende personer.
Analyse av forskjeller i frekvenser
Når utfallene er todelte (dikotome), f.eks. frisk eller syk, kan en beregne sammenheng mellom tiltaket og utfallet. Det er ulike måter å presentere resultatet, men utgangspunktet for analysene er alltid en 2x2 tabell. Tabell 1 er en 2x2 tabell som oppsummerer resultater fra en studie som undersøkte effekten av massasje for pasienter med kroniske nakkesmerter og viser at 18 av 31 (58 %) pasienter som fikk massasje ble bedre, mens 2 av 29 (7 %) pasienter i kontrollgruppen rapporterte bedring.
Tabell 1: Antall pasienter som rapporterte bedring ved 4 uker
| Bedring (Ja) | Ikke bedring (Nei) | Totalt | |
|---|---|---|---|
| Massasje (Tiltak) | 18 | 13 | 31 |
| Informasjon (Kontroll) | 2 | 27 | 29 |
| Totalt | 20 | 40 | 60 |
I de første kolonnene i tabell 2 er tallene fra tabell 1 presentert som prosent. En vanlig måte å analysere tallene er å se på forskjell i ”risikoen” for å bli bedre hvis du får massasje, sammenlignet med om du får en informasjonsbrosjyre. Risikoforskjellen mellom de to gruppene kan tallfestes, og er et punktestimat. Rundt effektestimat beregner vi et konfidensintervall (KI) som viser i hvilket intervall vi med sikkerhet kan si at effektestimatet ligger hvis vi skal anvende den i utgangspopulasjonen. Det er vanlig å oppgi KI med 95 % sikkerhet (95 % KI).
I denne videoen laget for KBP på tvers ved Høgskulen på Vestlandet får du en forklaring på konfidensintervall (2:30 min)
I denne videoen laget for KBP på tvers ved Høgskulen på Vestlandet får du en forklaring på risiko (1:52 min)
P-verdien viser sannsynligheten for at resultatet skyldes tilfeldige feil. Vi sier som regel at en p-verdi under 0,05 er statistisk signifikant, som betyr at sannsynligheten for at det skyldes tilfeldige feil er lav nok. Statistisk signifikans betyr ikke at resultatet er klinisk signifikant, det vil si om forskjellen betyr noe for pasienten.
I denne videoen laget for KBP på tvers ved Høgskulen på Vestlandet får du en forklaring på p-verdi (3:12 min)
Tabell 2: Analysere tall relativ risiko (RR) og 95 % KI (analyse av forskjell i frekvenser)
| Generell bedring | Massasje | Informasjon | Relativ risiko | 95 % KI | p-verdi |
|---|---|---|---|---|---|
| 4 uker | 58 | 7 | 8,5 | 2,0 til 35,4 | 0,003 |
| 26 uker | 43 | 25 | 1,8 | 0,8 til 3,8 | 0,14 |
I tabell 2 er risikoforskjellen mellom massasjegruppen og informasjonsgruppen presentert som relativ risiko (RR). For å finne RR må en regne ut risikoen i hver gruppe først. Risikoen i hver gruppe regnes ut ved å ta antallet som ble bedre, delt på alle i gruppen. I tiltaksgruppen ble 18 av 31 bedre, dvs. risikoen er 18/31 (58 %). I kontrollgruppen ble 2 av 29 bedre, dvs. risikoen er 2/29 (7 %). Tallene ble hentet fra Tabell 1. Den relative risikoen (RR) finner en ved å ta risikoen i tiltaksgruppen og dele på risikoen i kontrollgruppen, dvs. 58 delt på 7 som er 8,5. Det betyr at sjansen for å bli bedre var 8,5 ganger større for de som fikk massasje. I tabell 2 er RR presentert for alle måletidspunktene. Det er stor variasjon i 95 % KI for 4 uker (2,0 til 35,4), og p-verdien er 0,003. Ved 26 uker krysser konfidensintervallet 1 og p-verdien over 0,05, og den varige effekten er derfor usikker.
Resultatene kan også presenteres som absolutt risikoreduksjon (ARR) som angir andelen pasienter som ikke får et ugunstig utfall. Hvis vi tar utgangspunkt i 2×2 tabellen igjen (tabell 1) finner du ARR ved å ta risikoen for de som ikke fikk behandling (2/29) minus risikoen for de som fikk behandlingen (18/31). ARR blir da 7 % – 58 % = -51 % som betyr at sjansen (”risikoen”) for å bli bedre er 51 % større i tiltaksgruppen enn i kontrollgruppen etter fire uker.
En mer konkret måte å presentere resultatene på, er å si hvor mange som må få behandling for at én pasient skal bli bedre, evt. forhindre et ugunstig utfall. Denne måten kalles number-needed-to-treat (NNT). Dette regnes ut ved å ta 100 delt på absolutt risikoreduksjon (ARR) i prosent. I vårt eksempel er ARR 51 % slik at det blir 100/51. Det betyr, kort sagt, at hvis to pasienter får massasje vil én oppgi bedring etter fire uker.
Analyse av forskjeller i gjennomsnitt
Når utfallene er kontinuerlige, f.eks. målt på en visuell analog skala (VAS), kan du beregne gjennomsnitt og standardavvik. Det er en beskrivelse av sentraltendens og spredning for utfallet blant personene som deltok i den aktuelle studien. I tabell 3 viser vi resultatene fra en studie som har sett på effekten av p-piller (tiltaksgruppe) , sammenlignet med placebopiller (kontrollgruppe) mot menstruasjonssmerter. Gjennomsnitt (M) og standardavvik (SD) for alle målepunktene både før og etter behandlingsstart (pre- og posttest) for henholdsvis tiltaks- og kontrollgruppen, er presentert.
Tabell 3: Gjennomsnitt, standardavvik, 95 % KI og p-verdi for smerteskår
| P-piller tiltaksgruppe | Placebo kontrollgruppe | 95 % KI | p-verdi | |||
|---|---|---|---|---|---|---|
| Menstruasjonssmerter | M | SD | M | SD | ||
| Pretest | 11,1 | 5 | 11,8 | 5 | - | 0,53 |
| Posttest (3 måneder) | 3,1 | 3,2 | 5,8 | 4,5 | 0,88 til 453 | 0,004 |
I tabell 3 er det gjennomsnittene på posttestene som sammenlignes (her 3,1 og 5,8 for variabelen menstruasjonssmerter). I massasjestudien presenteres gjennomsnittsforskjellen sammen med konfidensintervall og p-verdi (tabell 4). For å kunne vurdere om endring er klinisk relevant, er det viktig å vite bredden på måleskalaen og ha et forhold til hva som er en viktig endring for pasienten. Hvis konfidensintervallet krysser 0 (gjelder kontinuerlige variabler) betyr det at det ikke er sikkert at det er forskjell i utgangspopulasjonen.
Tabell 4: Forskjell i gjennomsnitt og 95 % KI
| Symptombelastning | Gjennomsnittsforskjell | 95 % KI | p-verdi |
|---|---|---|---|
| 4 uker | -2,1 | -4,0 til -0,03 | 0,0006 |
| 26 uker | -4,4 til 0,63 | 0,14 |
I denne studien er gjennomsnittsforskjellen for symptombelastning ved fire uker mellom de som fikk massasje og de som fikk informasjon 2,1 poeng i favør av massasjegruppen. Utfallet er målt på en 0 til 10 poengs skala, og jo lavere skår desto bedre. 95 % KI i fire uker går fra minus 4 til minus 0,03 poeng. Det betyr at denne forskjellen kan overføres til utgangspopulasjonen. Ved oppfølging etter både 10 og 26 uker krysser konfidensintervallet 0. Da kan vi ikke si at forskjellen gjelder i utgangspopulasjonen.
I eksemplene over har vi valgt å vise til studier som sammenligner forskjeller i gjennomsnitt mellom en tiltaksgruppe og en kontrollgruppe. Det er viktig å være klar over at statiske analyser basert på gjennomsnittsforskjeller, kan gi feilaktige resultater hvis måleresultatene ikke er normalfordelte. I slike tilfeller kan det være aktuelt å benytte seg av andre statistiske metoder som for eksempel ikke-parametriske analyser og transformasjoner. Det finnes også statistiske metoder for å analysere data fra ikke-kontrollerte studier, for eksempel før-etter-studier, men det er viktig å være klar over at resultater fra ukontrollerte studier er utsatt for påvirkning fra systematisk feilkilder.
Eva Denison, Kunnskapssenteret, gir en innføring i hvordan analysere tall. Eva underviser i statistikk og kunnskapsbasert praksis for helsepersonell. I tillegg skriver hun kunnskapsoppsummeringer m.m. og har skrevet bruksanvisninger for ulike statistikkprogram.
Vær oppmerksom på feil to steder i videoen:
- Ved 4 min, 30 sek står det «Gjennomsnittsforskjellen mellom gruppene er 30 mmHg», mens det sies at den er 35 mmHg. Det korrekte er 30 mmHg.
- Ved 6 min, 11 sek står det «Risiko i eksperimentgruppen (Pille A): 18/46 = 0,28 = 28 %», mens det sies at det var 18 av 64 som fikk hjerteinfarkt. Det korrekte er 18/64 = 0,28 = 28 %.
4.8.4 Formidle tall
Sist faglig oppdatert: 11.06.2017
Når resultater fra et forskningsprosjekt formidles i en vitenskapelig artikkel har forfatterne begrenset plass. Forfatterne må prioritere hvilke data de vil presentere. Denne prosessen kan føre til skjevfremstilling av resultater og mangelfull rapportering av detaljer. I grafiske fremstillinger kan samme resultat tydeliggjøres og usynliggjøres ved å justere figurens layout. Tilsvarende kan oppfatningen av resultatene i en studie avhenge av hvilke tall (resultater) som trekkes frem og måten tallene presenteres på. Nedenfor viser vi to eksempler på hvordan tall kan presenteres.
Formidle forskjeller i gjennomsnitt
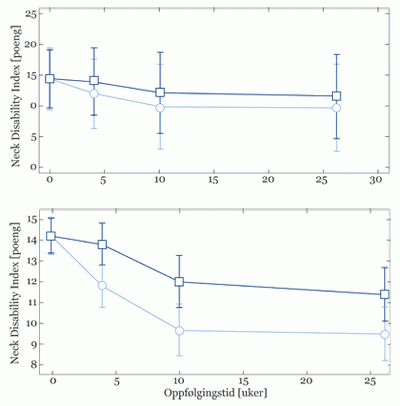
I forskningsartikler benyttes ofte figurer for å visualisere studiens resultater. Bruk av figurer fremmer lesbarheten. Samtidig kan dette påvirke leserens forståelse av resultatene i en retning som taler til studiens fordel. I figur 1 er resultatene som ser på effekter av massasje for hvordan nakkeproblemer påvirker hverdagsaktivitet, fremstilt grafisk. For å demonstrere at enkle layoutmessige virkemidler kan påvirke leserens tolkning av resultatet har vi valgt å vise resultatene på to måter. Det eneste som skiller de to framstillinger er at de mest interessante delene av figurene er forstørret i figuren til høyre, samtidig som standardavvik (vertikale linjer) er byttet ut med tilhørende standardfeil. Ville du blitt lurt av våre virkemidler?
Figur 1 Samme datasett, to ulike grafiske framstillinger
Formidle forskjeller i frekvens
I modulen om analyse av tall så vi at resultatet kan presenteres på ulike måter selv når utfallet er todelt (ja/nei). De ulike effektstørrelser (for eksempel relativ risiko og odds ratio) baserer seg på det samme tallmaterialet, men har ulike styrker og svakheter. Hvilke effektestimat som presenteres i en artikkel kan ha stor betydning for hvordan leseren oppfatter resultatene. I tabell 1 illustrerer vi dette ved å se på to ulike studier, og for hver av studiene har vi beregnet fire ulike effektestimat (OR, RR, ARR og NNT):
Tabell 1 Resultat presentert ved hjelp av ulike effektstørrelser
| Effektstørrelse | Artikkel 1 | Artikkel 2 |
|---|---|---|
| Odds Ratio [95 % CI] | 0,38 [0,22 til 0,67] | 0,16 [0,06 til 0,48] |
| Risk Ratio [95 % CI] | 0,39 [0,22 til 0,68] | 0,69 [0,55 til 0,86] |
| ARR [95% CI] | 0,6 % [0,3 til 0,7] | 28 % [13 til 41] |
| NNT [95 % CI] | 172 [143 til 333] | 3,5 [2,4 til 7,7] |
Bosch et al (2002) BMJ 324:699-702. Brent et al (1995) Arch Pediatr Adolesc Med 149: 788-803
En av de viktigste forskjellene på de to artiklene er hyppigheten av utfallet de måler (henholdsvis 9 per 1000 og 912 per 1000). Dette har betydning for hvordan de ulike effektstørrelsene forholder seg til hverandre. Ved lav forekomst ligger relative effektstørrelser (OR og RR) nært i verdi, mens ved høy forekomst vil OR gi mer ekstreme verdier enn RR. Det kan gi rom for misforståelser idet mange lesere tolker OR på samme måte som RR. Absolutte effektstørrelser (ARR og NNT) vil i mye større grad enn relative størrelser (OR og RR) reflektere forekomsten av utfallet som måles. Når man skal vurdere resultater kan det derfor være nyttig å sammenligne flere ulike effektestimat.
Statistisk forskjell er ingen forskjell før den utgjør en forskjell for pasienten
Av og til kan studier påvise små effektforskjeller mellom to tiltak. Det vil si at effekten av tiltaket som studeres ganske sikkert (> 95 %) er større enn null, men at effekten er for liten til å utgjøre en praktisk forskjell for pasientene (tabell 2).
Tabell 2 Ikke alle statistisk signifikante forskjeller er klinisk viktig
| Utfallsmål | Skala | Endring | Statistisk signifikant | Klinisk signifikant |
|---|---|---|---|---|
| Neck disability index | 0 til 50 | 2,1 | Ja | Tvilsomt |
| Symptombelastning | 0 til 10 | 1,6 | Ja | Sannsynlig |
I studien som undersøkte effekten av massasje hos pasienter med kroniske nakkesmerter, følte 8,5 ganger flere av pasientene i massasjegruppen seg bedre fire uker etter behandling, og tiltaket kan sies å være virkningsfullt både fra et statistisk (p<0,003) og et klinisk ståsted. Den samme studien så på hvordan nakkeproblemer begrenser hverdagsaktiviteter.
Gjennomsnittsforskjellen mellom gruppene ved fire uker er statistisk signifikant (p=0,047), men en forskjell på 2.1 poeng på en skala fra 0-50 betyr antageligvis lite for pasienten. Forskjellen i symptombelastning ved fire uker er også statistisk signifikant (p= 0,006), nærmere bestemt 1,6 poeng. Symptombelastningsskalaen som er brukt går fra 0-10 poeng, så her kan man tenke seg at forskjellen betyr noe for pasienten i hverdagen. Det viser at statistisk signifikans ikke nødvendigvis tilsier at et tiltak skal iverksettes. Helsepersonell og pasient må i fellesskap vurdere om gjennomsnittlig behandlingseffekt vil gjøre påvirke praksis. Potensiell effekt må også vurderes opp mot risiko for bivirkninger og opp mot totale behandlingskostnader (helseøkonomiske analyser).
Kjetil G. Brurberg, Kunnskapssenteret, forteller om utfordringer knyttet til formidling og forståelse av tall. Kjetil underviser i statistikk og kunnskapsbasert praksis, og han skriver kunnskapsoppsummeringer med mer.
4.8.5 Metaanalyse
Sist faglig oppdatert: 11.06.2017
Samle løse tråder
Utgangspunktet for enhver metaanalyse bør være en god systematisk oversikt som samler alle relevante studier. Hvis du finner flere studier som besvarer samme problemstilling vil hjernen straks lete etter mønstre. Så lenge alle tilgjengelige data trekker i samme retning settes du ikke på store prøver, men det er vanskeligere å forholde seg til sprikende (inkonsistente). Intuisjonen forteller deg kanskje at du bør telle opp antall studier med én bestemt konklusjon og stole på den konklusjonen som får flest stemmer. Ofte finnes det gode grunner til at noen studier bør tillegges større vekt enn andre, for eksempel fordi de involverer mange deltakere eller er godt gjennomført. I slike situasjoner er metaanalyser å foretrekke fremfor intuisjon og ”magefølelsestatistikk”.
Diamanten
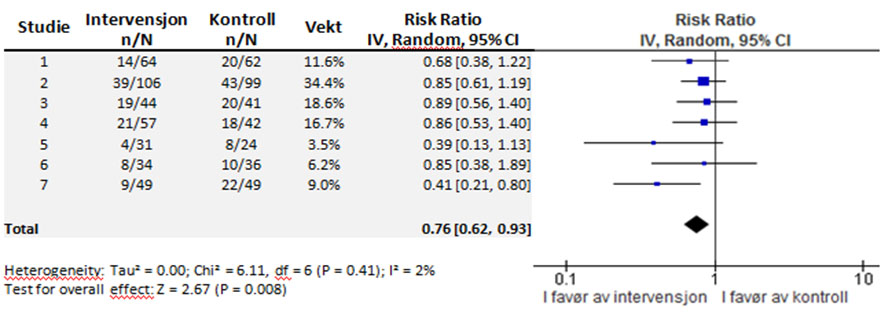
Metaanalyser forbindes gjerne med balansediagram (forest plot) der hver rad henviser til én enkeltstudie. Kolonnevis får du gjerne informasjon om de inkluderte enkeltstudiene, som for eksempel antall deltakere, i tillegg til en kolonne som forteller hvor stor vekt studien er tillagt i metaanalysen. Resultatet vises på nederste rad der sammenslått effektestimat ofte fremkommer som en diamant (Figur 1). Bredden på diamanten viser konfidensintervallet (spredning), mens midten av diamanten viser effektmålet (sentraltendens). Akkurat som i enkeltstudier kan du velge mellom ulike effektmål i en metaanalyse. Dikotome utfallsmål presenteres typisk i form av relativ risiko, odds ratio eller relativ risikoforskjell (jf. Analysere tall 1), og ved kontinuerlige utfallsmål er ofte gjennomsnittsforskjell (MD) å foretrekke (jf. Analysere tall 2). Du kan også komme over metaanalyser som beregner standardiserte gjennomsnittsforskjeller (SMD). SMD brukes for å slå sammen studier som har målt tilnærmet samme utfall på ulike skalaer, men SMD er ofte vanskelig å fortolke i praksis.
Figur 1 Metaanalyse, deksametason for tilbakevendende hodepine (Colman et al (2008) BMJ 336:1359-61)
Heterogenitet
Figur 1 viser et balansediagram med godt samsvar mellom alle inkluderte studier, men ofte vil du finne enkeltstudier med sprikende (heterogene) resultater. Heterogenitet refererer til variasjon mellom enkeltstudier som ikke kan tilskrives tilfeldigheter, men som heller har sin årsak i at enkeltstudiene faktisk er forskjellige, for eksempel fordi intervensjonen gis med varierende intensitet eller populasjonen er satt sammen på ulike vis. I metaanalyser måles heterogenitet ofte i form av et måltall som kalles I2 og tar verdier mellom 0 og 100 %. I2 viser hvor mye av den totale variasjonen som ikke kan forklares av tilfeldige feil. Med stigende I2 øker sjansen for at det er reelle forskjeller mellom de inkluderte studiene – en advarsel om at det muligens ikke er så lurt å slå sammen de aktuelle studiene.
De som gjennomfører en metaanalyse kan velge mellom en tilfeldig (random) eller fiksert (fixed) effektmodell. Her skal vi ikke gå i detaljer utover å nevne at forskjellen mellom de to modellene øker med stigende I2, og den randomiserte modellen er å foretrekke hvis du forventer å observere heterogenitet i en planlagt metaanalyse. Noen ganger er det aktuelt å gjøre subgruppeanalyser for å utforske heterogenitet. Dette kan være nyttig, men husk at subgruppeanalyser bør være definert i forkant (apriori) og helst være basert på en biologisk plausibel årsaksmekanisme.
Kjetil G. Brurberg, Kunnskapssenteret, forklarer hvorfor metaanalyser kan være hensiktsmessige og hvordan du skal forstå en metaanalyse. Presentasjonen er tilpasset lesere som har svært liten erfaring med metaanalyser fra tidligere.
5. Anvende
Sist faglig oppdatert: 25.02.2019
Å bruke forskningsbasert kunnskap i praksis er spennende og utfordrende. Denne prosessen kalles ofte kunnskapstranslasjon som er å overføre forskningsbasert kunnskap til handling i praksis. Et annet begrep er implementering.
Viktige elementer for å bruke forskning i praksis er:
- God tilgang til forskningslitteratur
- Økt kunnskap i å forstå forskning
- Ledelsesforankring og kollegial støtte
- Oppmuntring til å anvende forskning i praksis
Gro Jamtvedt, OsloMet – storbyuniversitetet, gir deg mer informasjon om implementering av KBP. Gro underviser i KBP og har skrevet lærebøker om emnet:
5.1 Kunnskap til handling
Sist faglig oppdatert: 29.02.2024
Kunnskap-til-handling-modellen er et implementeringsverktøy. Registered Nurses' Association of Ontario (RNAO) har utviklet en verktøykasse for å hjelpe helsepersonell å overføre forskningsbasert kunnskap til praksis Verktøykassen er oversatt til norsk og tilpasset til norske forhold. Utgangspunktet er forskningsbasert kunnskap, fra for eksempel systematiske oversikter eller kunnskapsbaserte retningslinjer, som brukes inn i kunnskap-til-handling-modellen. Den forskningsbaserte kunnskapen må integreres med erfaringsbasert kunnskap, pasientkunnskap og kontekst og egnede implementeringsstrategier må velges. Fasene i Kunnskap-til-handling-modellen er arbeid med interessenter, ressurser, barrierer og motivasjonsfaktorer samt å skreddersy en konkret implementeringsplan.
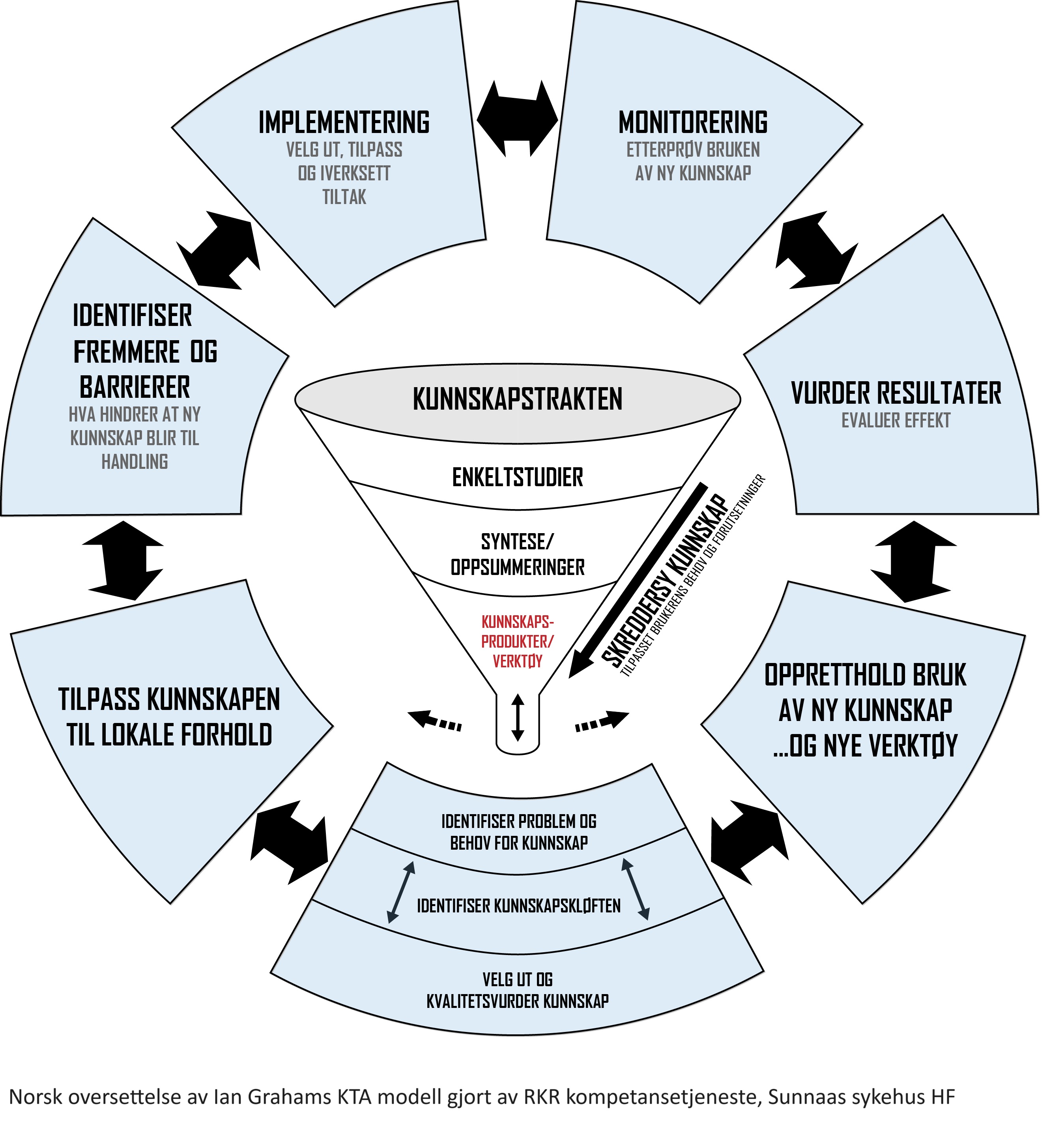
Kunnskap-til-handling-modellen (kunnskapstranslasjon) komplementerer kunnskapsbasert praksis-modellen. Det er ikke fullstendig overlapp mellom disse modellene, for eksempel kalles innhenting og vurdering av forskning kunnskapstrakten i kunnskap-til-handling-modellen. Kunnskapstrakten sammen med den første fasen dekker de fire første trinnene i kunnskapsbasert praksis: 1) refleksjon, 2) spørsmålsformulering, 3) litteratursøk og 4) kritisk vurdering. Kunnskap-til-handling-modellen er nyttig for å konkretisere de neste to trinnene 5) anvende og 6) evaluere. Regional kompetansetjeneste for rehabilitering (RKR) ved Sunnaas sykehus har utviklet og bruker denne videoen til opplæring i kunnskapstranslasjon (8:25 min):
Video laget av Regional kompetansetjeneste for rehabilitering, brukt med tillatelse.
5.1.1. Identifisere problem og behov for kunnskap
Den første fasen i kunnskap-til-handling-modellen er å identifisere et problem eller behov for forskningsbasert kunnskap. Behovet kan for eksempel oppstå som resultat av at noe ikke fungerer eller at det er kommet ny forskning, nye retningslinjer eller fagprosedyrer som krever endring i praksis. Kløften mellom eksisterende praksis og forskningsbasert kunnskap må identifiseres og analyseres. I denne prosessen er det nyttig å engasjere pasientnære medarbeidere og spørre dem om det er en kløft mellom eksisterende praksis og mønsterpraksis. I kapittel 1 i verktøykassen for implementering av kunnskapsbaserte retningslinjer finnes et verktøy for å avdekke kunnskapskløfter.
5.1.2. Tilpasse kunnskapen til lokale forhold
For å tilpasse den forskningsbaserte kunnskapen til lokale forhold må interessenter identifiseres, analyseres og engasjeres. Interessenter omfatter enkeltpersoner eller grupper som kan påvirke eller blir påvirket av implementeringen. Identifisering av interessenter kan gjøres på flere måter, for eksempel ved å bruke snøballteknikken som innebærer å be alle du tror er interessenter om å identifisere andre interessenter. Interessentanalysen kartlegger interessentenes egeninteresse, inflytelse, motivasjonsfaktorer og barrierer for foreslåtte endringer. Interessentenes engasjement samt økonomiske og menneskelige ressurser er viktige faktorer for en vellykket implementering. Du kan lese mer om dette i kapittel 2 i verktøykassen for implementering av kunnskapsbaserte retningslinjer
5.1.3 Identifisere og vurdere motivasjonsfaktorer og barrierer
Identifisering og forståelse av motivasjonsfaktorer og barrierer er avgjørende for å lage en god implementeringsplan. Motivasjonsfaktorer kan være støtte fra ledelsen, samarbeid og nettverk på tvers og personlig interesse for forbedring. Barrierer kan for eksempel være negative holdninger til endring hos medarbeidere og uenighet om faglig innhold. Motivasjonsfaktorer og barrierer kan endres i løpet av implementeringsfasen og det som er motiverende for en kan være en barriere for en annen, for eksempel det å ta i bruk elektroniske verktøy. Du kan lese mer om dette i kapittel 3 i verktøykassen for implementering av kunnskapsbaserte retningslinjer.
5.1.4 Velge og skreddersy intervensjoner og strategier for implementering
Det finnes ulike strategier for implementering, for eksempel opplæringsmateriell, opplæringsmøter, praksisbesøk samt audit og feedback. Forskningen er ikke entydig på hvilke tiltak som er mest effektive, men det ser ut til at kombinasjon av flere virkemidler kan resultere i praksisendring. Det er viktig å ta hensyn til lokale forhold og de identifiserte motivasjonsfaktorer og barrierer når man velger implementeringsstrategier. Du kan lese mer om dette i kapittel 4 i verktøykassen for implementering av kunnskapsbaserte retningslinjer.
5.2 Samvalg
Sist faglig oppdatert: 17.09.2021
Samvalg er det norske begrepet for «shared decision making» og defineres som en felles beslutningsprosess hvor den forskningsbaserte kunnskapen, helsepersonells erfaringer og brukerens erfaring og preferanser brukes aktivt for å ta et informert valg.
Samvalg skjer når pasienten får informasjon om fordeler og ulemper ved ulike undersøkelses- og behandlingsalternativer, vurderer disse opp mot hverandre med aktiv støtte av helsepersonell og trekker fram hva som er viktig for den enkelte pasient Denne videoen fra Samvalgssenteret på Universitetssykehuset Nord-Norge viser dette fra pasientens ståsted.

Hva samvalg er og hvordan det kan gjøres i praksis snakker Simone M. Kienlin og Magne Nylenna om i denne podkasten (14 minutter).
De beskriver stegene i samvalg:
Problem - Kjernebudskap - Alternativer - Avveiing - Beslutning - Avtaler
Mer om samvalg
Elwyn G, Frosch D, Thomson R, Joseph-Williams N, Lloyd A, Kinnersley P, et al. Shared decision making: a model for clinical practice. Journal of general internal medicine. 2012;27(10):1361-7.
Hoffmann TC, Montori VM, Del Mar C. The connection between evidence-based medicine and shared decision making. Jama. 2014;312(13):1295-6.
Nasjonale samvalgsverktøy er samlet på HelseNorge.no.
Engelskspråklige samvalgsverktøy samlet av the Ottawa Hospital Research Institute.
Hva er viktig for deg? - En retningsendring. Artikkel fra Folkehelseinstituttet.
5.3 Retningslinjer og fagprosedyrer
Sist faglig oppdatert: 13.02.2020
Retningslinjer
Helsepersonell trenger tilgang til råd og anbefalinger i kunnskapsbaserte faglige retningslinjer for å sikre pasienter riktig diagnose, pleie og behandling. Eksisterende retningslinjer er ikke alltid utviklet i tråd med nye definisjoner og standarder for kunnskapsbaserte faglige retningslinjer.
GRADE (Grading of Recommendations Assessment, Development and Evaluation) brukes for å vurdere tilliten til resultatene i en systematisk oversikt og styrken anbefalingene i en retningslinje1
Per Olav Vandvik, Universitetet i Oslo og Lovisenberg diakonale sykehus, forteller i denne videoen hvordan GRADE kan brukes å vurdere kvalitet på dokumentasjonen og angi styrke på anbefalinger i retningslinjer (4:03).
- Folkehelseintituttet. (2022, 22. april). Slik oppsummerer vi forsking. Hente ut data, sammenfatte og gradere.Folkehelseinstituttet. https://www.fhi.no/nettpub/metodeboka/effekt-av-tiltak/hente-ut-data-sammenfatte-og-gradere/
Fagprosedyrer
Hensikten med en klinisk prosedyre er å sikre at en handling i klinisk praksis utføres i henhold til pasientens preferanser, de beste tilgjengelige forskningsresultatene og klinisk erfaring.
Kliniske prosedyrer er bruksanvisninger for handlinger som skal utføres. Prosedyren fastlegger ansvar og beskriver handlingen. Avviksregistrering kan knyttes til prosedyrene.
En prosedyre kan utarbeides av alle faggrupper. I noen miljøer utvikler forskere, helsepersonell og pasienter prosedyrer sammen. AGREE-verktøyet kan brukes både i utvikling og kritisk vurdering av prosedyrer og retningslinjer.
5.4 Jobbe kunnskapsbasert
Sist faglig oppdatert: 17.09.2021
En måte å implementere kunnskapsbasert praksis på arbeidsplassen er å opprette fagringer. Haukeland universitetssykehus var først ute med å innføre fagringer blant sykepleiere ved tre avdelinger. Inspirert av dette prosjektet har kommunehelsetjenesten i Bergen satt i gang fagringer lokalisert på Løvåsen sykehjem, Undervisningssykehjem. Hensikten er å lære seg å arbeide kunnskapsbasert og å implementere forskning i praksis for å kunne gi pasientene bedre helsetjenester.
Fagringer settes sammen av 3-5 deltakere. Gjennom et år arbeides det med én konkret problemstilling som er relevant for deltakerne og deres praksis. Det innhentes forskningslitteratur, artikler/retninglinjer vurderes kritisk i henhold til sjekklister og det lages en implementeringsstrategi før det hele evalueres.
Suksessfaktorer:
- God organisering og planlegging
- Ledelsesforankring
- Undervisningsdager og veiledning underveis i arbeidsperioden
- Avsatt tid
Liv Irene Ruud, Høgskulen på Vestlandet, presenterer fagringer fra et undervisningssykehjem (5:54 min).
5.5 Opplæring
Sist faglig oppdatert: 24.02.2019
For all høyere utdanning er det en utfordring å forberede studenter på en yrkesutøvelse som er i kontinuerlig endring. Stadig ny viten og nye krav til kompetanse og teknologi må møtes med et utdanningsforløp som kan forberede dynamiske og selvstendige utøvere av sin profesjon.
I Nasjonal strategi for kvalitetsforbedring i sosial og helsetjenestene heter det at helsevesenet i større grad må kunne ta i bruk ny og relevant kunnskap. Dette er krav som sammenfaller med nøkkelelementer i konseptet kunnskapsbasert praksis. Gjennom flere år har bachelorutdanning ved Høgskolen i Bergen systematisk implementert kunnskapsbaserte prinsipper gjennom en treårig utdanning (fysioterapi og radiografi). Erfaringsmessig har kunnskapsbasert praksis (KBP) vært egnet til å bli kombinert med den pedagogiske tanken om problembasert læring.
Tidlig i studiet blir studentene presentert for KBP gjennom en innføring i konseptet. Behovet for å bruke forskning i fagutøvelsen blir synliggjort tidlig, og blir fulgt opp gjennom tilbud om kurs i litteratursøk av bibliotekar. Studentene møter krav om at denne tilnærmingsformen anvendes gjennom studiet, gjennom integrering av forsknings- og erfaringsbasert kunnskap, men også med fokus på kritisk anvendelse av forskningslitteratur.
Planlegger du å undervise i kunnskapsbasert praksis? Her får du noen enkle råd ved Nina Rydland Olsen, Høgskulen på Vestlandet (5:19 min):
6. Evaluere praksis
Sist faglig oppdatert: 13.09.2022
Evaluering av praksis er siste trinn i sirkelen for kunnskapsbasert praksis. Det er viktig å evaluere praksis i helsetjenesten.
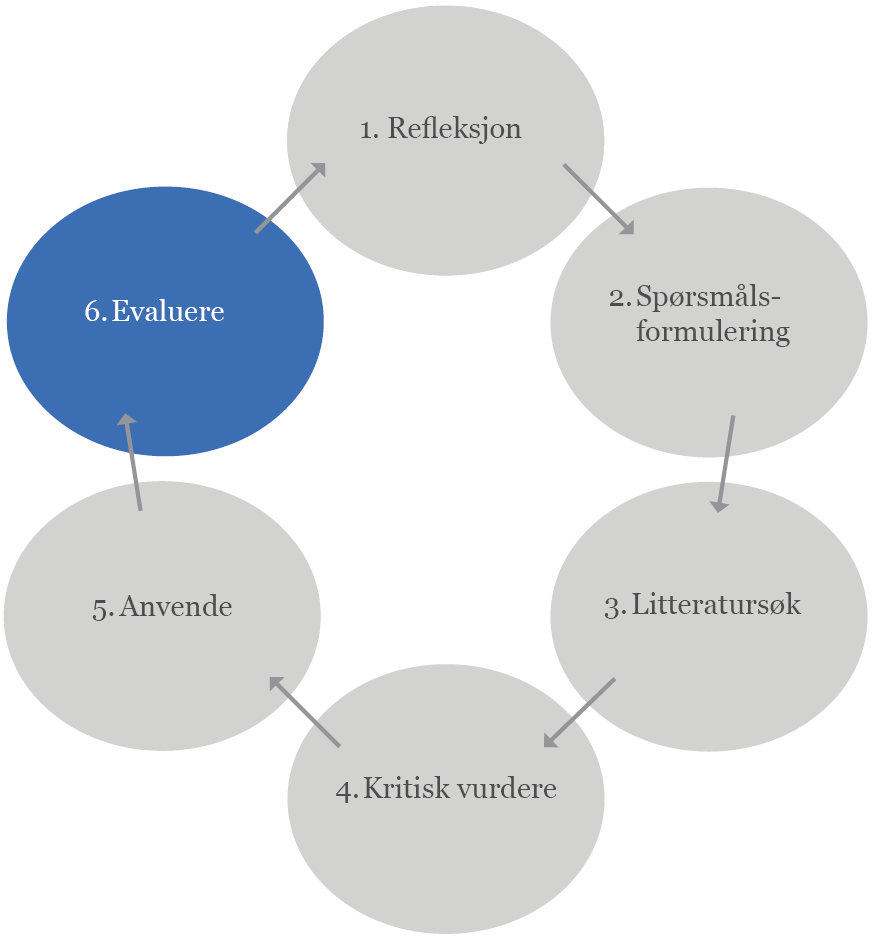
Kvalitetsforbedring er en kontinuerlig prosess som omhandler å forbedre områder i helse- og omsorgstjenesten. Å jobbe systematisk med kvalitetsforbedring er viktig. Det finnes mange metoder og verktøy for å få til forbedringer, men ingen enkle løsninger.
Du kan for eksempel spørre deg selv om du jobber kunnskapsbasert. Det samme kan pasienter, kolleger, samarbeidspartnere og de som finansierer tjenestene.
Kvalitetsindikatorer er en av flere metoder som benyttes for å overvåke og dokumentere kvaliteten i helsetjenesten.
Evalueringen eller audit av klinisk praksis er en prosess i to faser. Første fase innebærer å måle hva som faktisk skjer i praksis, for så å sammenligne dette mot standarder eller andre eksplisitte kriterier i fase to.
| Selvevaluering – jobber jeg/vi kunnskapsbasert? | |
| Refleksjoner rundt praksis/bevissthet rundt praksis |
|
| Å stille spørsmål |
|
| Søke etter forskningslitteratur |
|
| Kritisk vurdering |
|
| Implementering av klinisk forskning |
|
| Selvevaluering |
|
Klinisk audit
Klinisk audit er en kvalitetsforbedringsmetode med mål om å forbedre helsetilbudet til pasienten.
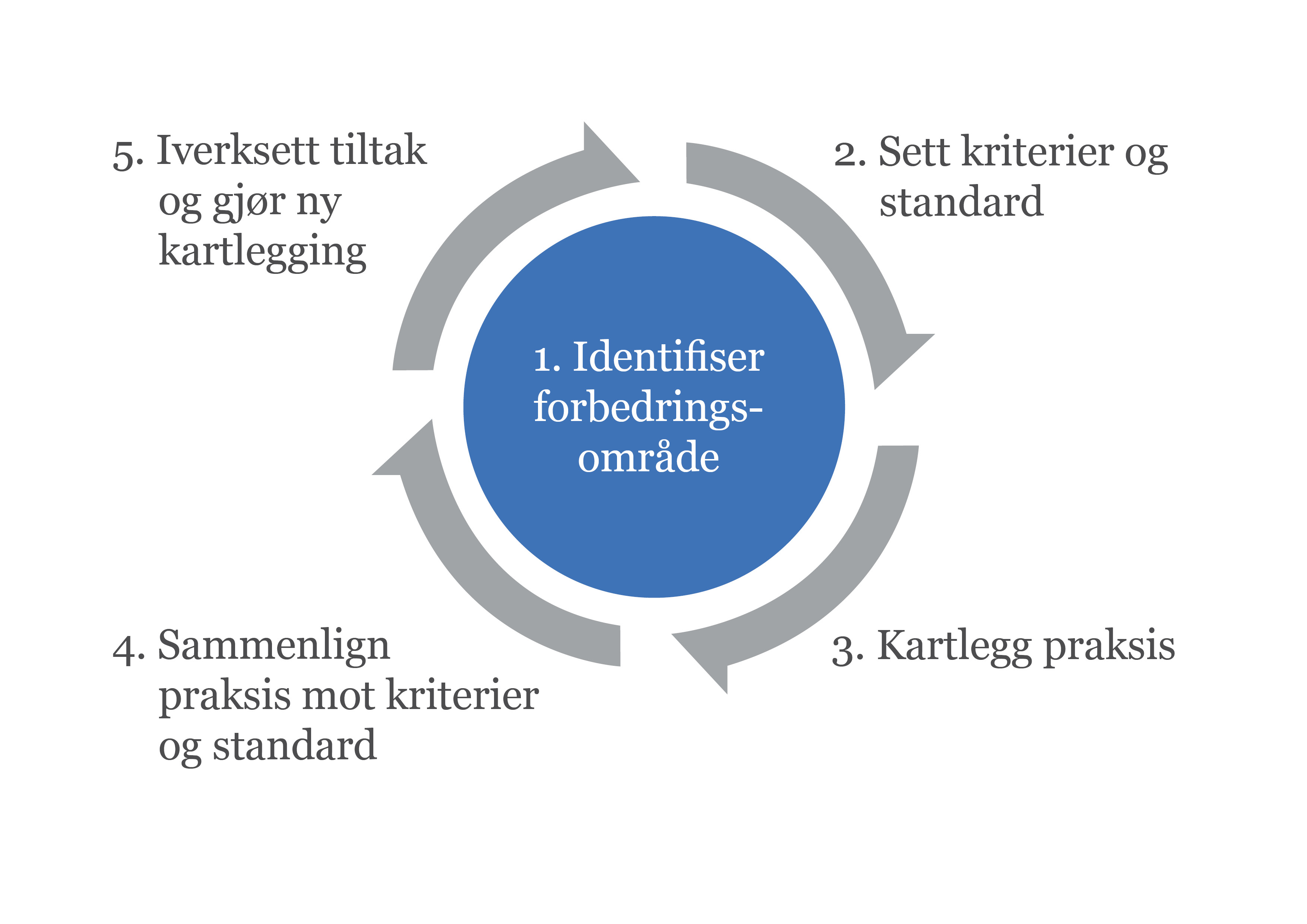
Hensikten er å evaluere i hvilken grad helsetjenestene møter kunnskapsbaserte anbefalinger for problemområdet som skal kvalitetsforbedres. Gjennom en audit kan man få kartlagt standarden på pasientbehandlingen, og få satt søkelys på eventuelle behov for forbedring. Resultatene fra kvalitetsvurderingen må formidles til praksis gjennom tilbakemelding, eller feedback. Da kalles det audit og feedback.
Katrine Aasekjær, høgskolelektor, Høgskolen i Bergen.
Kvalitetsindikatorer
Det bør stilles strenge krav ved utviklingen av kvalitetsindikatorer slik at de er gyldige, pålitelige og anvendbare. Et kjernepunkt i utviklingen er den systematiske tilnærmingen, som tar sikte på å ivareta både det vitenskapelige og faglige aspektet, og den helsepolitiske og verdimessige dimensjonen. Det bør legges stor vekt på legitimitet og faglig forankring i seleksjonsprosessene (transparens). Formaliserte konsensusprosesser som vurderer den forskningsbaserte kunnskapen i kombinasjon med kollektive ekspert- og brukervurderinger, er en mye brukt tilnærming for å bidra til dette1.
- Folkehelseintituttet. (2018, 09. april). Hva kjennetegner gode kvalitetsindikatorer? Kvalitetsforbedring. https://www.helsebiblioteket.no/kvalitetsforbedring/kvalitetsmaling/hva-kjennetegner-gode-kvalitetsindikatorer
Litteratur
Sist faglig oppdatert: 17.09.2021
Artikler
Alper, B. S., & Haynes, R. B. (2016). EBHC pyramid 5.0 for accessing preappraised evidence and guidance. Evidence-Based Medicine, 21(4), 123-125.
Austvoll-Dahlgren, A., & Johansen, M. (2013). Pasienten som medvirker og kunnskapshåndterer. Norsk Epidemiologi, 23(2), 225-230.
Denison, E. (2013). Kunnskapsbasert folkehelse - eksempel fysisk aktivitet. Norsk Epidemiologi, 23(2), 181-185.
DiCenso, A., Bayley, L., & Haynes, R. B. (2009). Accessing preappraised evidence: fine-tuning the 5S model into a 6S model. Annals of Internal Medicine, 151(6), JC3-2.
Faber Frandsen, T., Dyrvig, A.-K., Buck Christensen, J., Fasterholdt, I., & Oelholm, A. M. (2014). En guide til valide og reproducerbare systematiske litteratursøgninger. Ugeskrift for Laeger, 176(7), 647-651.
Flottorp, S., & Aakhus, E. (2013). Implementeringsforskning: vitenskap for forbedring av praksis. Norsk Epidemiologi, 23(2), 187-196.
Fretheim, A. (2013). Kunnskapsbasert politikkutforming. Norsk Epidemiologi, 23(2), 205-210.
Fretheim, A. (2013). Medisinsk kunnskap før og nå: Fra teori til systematiske oversikter. Norsk Epidemiologi, 23(2), 113-118.
Fure, B., Lauvrak, V., Arentz-Hansen, H., Skår, Å., Ormstad, S. S., Vang, V. J., & Frønsdal, K. B. (2013). Metodevurderinger: Kunnskapsbasert beslutningsstøtte på overordnet nivå i helsetjenesten. Norsk Epidemiologi, 23(2), 165-169.
Fure, B., Ormstad, S. S., Vang, V. J., Lauvrak, V., Frønsdal, K. B., Skår, Å., & Arentz-Hansen, H. (2013). Mini-metodevurdering: Rask og trygg innføring av nye metoder i sykehus. Norsk Epidemiologi, 23(2), 171-175.
Glasziou, P., & Heneghan, C. (2009). A spotter's guide to study designs. Evid Based Med, 14(2), 37-38.
Glenton, C., & Rosenbaum, S. (2013). Cochrane i Norge - Hvordan formidler vi resultatene fra Cochrane-oversikter? Norsk Epidemiologi, 23(2), 215-219.
Jamtvedt, G. (2013). Systematiske oversikter om effekt av tiltak. Norsk Epidemiologi, 23(2), 119-124.
Jamtvedt, G., & Hagen, K. B. (2015). Brukermedvirkning og kunnskapsbasert fysioterapi. Fysioterapeuten, 82(2), 30-33.
Jamtvedt, G., Lund, H., & Nortvedt, M. W. (2014). Kunnskapsbasert forskning? Tidsskrift for den Norske Laegeforening, 134(1), 10-11.
Kirkehei, I., & Ormstad, S. S. (2013). Litteratursøk. Norsk Epidemiologi, 23(2), 141-145.
Liland, H.-I., Moe, V., Thomassen, S., & Lind, R. (2017). Jobber og underviser kunnskapsbasert. Sykepleien.
Mathisen, M., Hjelmesæth, J., Aune, E., Ruddox, V., & Otterstad, J. E. (2013). Tidsskriftet bør stille strengere krav til litteratursøk. Tidsskrift for den Norske Lægeforening, 133(15), 1615-1617.
Munabi-Babigumira, S., Johansen, M., & Paulsen, E. (2013). Den norske EPOC-satellitten: støtte til kunnskapsbaserte beslutninger. Norsk Epidemiologi, 23(2), 211-214.
Noonan, E. (2013). Campbell Collaboration og arbeidet for å fremme kunnskapsbasert sosialpolitikk. Norsk Epidemiologi, 23(2), 177-180.
Olsen, N. R. (2016). Kunnskapsbasert praksis i fysioterapiutdanning. Fysioterapeuten, 83(8), 36.
Ormstad, S. S., & Underdal, H. (2013). Informasjonskilder for kunnskapsbasert praksis. Norsk Epidemiologi, 23(2),
Ringerike, T., Glenton, C., Vist, G. E., Jamtvedt, G., & Nylenna, M. (2013). Tolker leserne forskningsresultater i tråd med forfatternes intensjoner? Norsk Epidemiologi, 23(2), 231-236.
Smedslund, G. (2013). Metaanalyse. Norsk Epidemiologi, 23(2), 147-149.
Strømme, H. (2017). Kilder til forskningsbasert kunnskap. Sykepleien Forskning, (2).
Strømme, H. (2017). Litteratursøking i kunnskapsbasert praksis og forskning. Sykepleien Forskning, (2).
Underdal, H., & Langengen, I. W. (2017). Jakten på svar. Sykepleien Forskning, (2).
Vandvik, P. O., Berg, R., & Vist, G. (2013). En ny generasjon troverdige kliniske retningslinjer. Norsk Epidemiologi, 23(2), 197-204.
Vist, G. E., Sæterdal, I., Vandvik, P. O., & Flottorp, S. A. (2013). Gradering av kvaliteten på dokumentasjonen. Norsk Epidemiologi, 23(2), 151-156.
Bøker
Bjørndal, A. (2013). Kunnskapshåndtering i medisin og helsefag (3. utg.). Oslo: Gyldendal akademisk.
Dudley-Brown, S., & White, K. M. (2012). Translation of evidence into nursing and health care practice. New York: Springer.
Elinder, L. S., & Kwak, L. (2014). Evidensbaserat folkhälsoarbete. Lund: Studentlitteratur.
Elwyn, G., Edwards, A., & Thompson, R. (2016). Shared decision making in health care : achieving evidence-based patient choice (3. utg.): Oxford University Press.
Graham, I. D., Straus, S. E., & Tetroe, J. (2013). Knowledge translation in health care : moving from evidence to practice (2. utg.). Chichester: Wiley-Blackwell.
Greenhalgh, T. (2014). How to read a paper : the basics of evidence-based medicine (5. utg.). Chichester: John Wiley.
Jamtvedt, G. (2015). Kunnskapsbasert fysioterapi : metoder og arbeidsmåter (2. utg.). Oslo: Gyldendal akademisk.
Liamputtong, P. (2013). Research methods in health : foundations for evidence-based practice (2. utg.). Melbourne, Australia: Oxford University Press.
Nortvedt, M. W., Graverholt, B., Jamtvedt, G., & Gundersen, M. W. (2021). Jobb kunnskapsbasert! : en arbeidsbok (3. utg.). Cappelen Damm akademisk.
Woloshin, S., Schwartz, L. M., & Welch, H. G. (2008). Know Your Chances: Understanding Health Statistics.
Verktøy
Her finner du verktøy som kan være nyttige når du skal lære eller lære kunnskapsbasert praksis.
KBP-læringsverktøy
KBP-læringsverktøy er et verktøy for å jobbe kunnskapsbasert og dokumentere prossessen.
EBP Steps
EBP Steps er en app for deg som skal lære å anvende kunnskapsbasert praksis, enten du er student eller kliniker. Appen gjør ikke jobben for deg, men hjelper deg å strukturere og dokumentere prosessen med trinnene i kunnskapsbasert praksis: Refleksjon, spørsmålsformulering, litteratursøk, kritisk vurdering, anvendelse og evaluering.
Les mer og last ned appen: EBP Steps
E-læringskurs
Sist faglig oppdatert: 25.02.2021
E-læringskurs i kunnskapsbasert praksis.
Kurset er utviklet for leger i spesialisering, men kan tas av alle. Det er tilgjengelig i de regionale helseforetakenes læringsportaler. Hvis du er ansatt i et helseforetak, anbefaler vi at du tar kurset via læringsportalen slik at det blir registrert at du har gjennomført kurset. Noen av læringsportalene gir mulighet for innlogging som ekstern bruker med tilhørende dokumentasjon av gjennomførte kurs. Hvis du ikke har tilgang til en slik læringsportal kan du ta kurset via lenkene under. Denne gjennomføringen blir da ikke dokumentert.
Kurset består av en rekke delkurs, hvorav et med flere moduler. Innholdet er hentet fra kunnskapsbasertpraksis.no og er tilpasset til e-læring av e-læringskoordinatorer Lena Marie Haukom, Sørlandet sykehus og Bente Langvik Olsen, Sykehuset Innlandet i samarbeid med Irene Wiik Langengen og Hilde Strømme, Folkehelseinstituttet. Hele kurset tar 4-5 timer å gjennomføre.
Merk! Innholdet på nettsidene er mer oppdatert enn e-læringskursene. Hvis du ikke har behov for å få registrert at du har tatt kurset gjennom en læringsportal bør du vurdere å gå gjennom innholdet på nettsidene fremfor å se på e-læringskursene.
Kurs 1: Introduksjon
Gjennomføringstid: ca. 15 minutter.
Kurs 2: Refleksjon og spørsmålsformulering
Gjennomføringstid: ca. 30 minutter.
Kurs 3: Litteratursøk
Gjennomføringstid: ca 40 minutter.
Kurs 4: Kritisk vurdering
Kritisk vurdering er et stort tema, og kurset er derfor delt opp i to deler. Del A handler om kritisk vurdering av ulike typer studier, og er delt opp i syv moduler. Hver modul tar mellom 10 og 15 minutter å gjennomføre. Øvelsesoppgaver i å vurdere artikler er ikke medregnet. Del B handler om statistikk og tar ca. 40 minutter å gjennomføre.
Kurs 4B: Kritisk vurdering - statistikk
Kurs 5: Anvendelse og evaluering
Gjennomføringstid: ca 35 minutter







