4.8.1 Beskrive tall

Statistikk er å analysere og beskrive ved hjelp av tall. Tallene kan beskrive hvor mange (som er syke), hvor ofte (opptrer symptomer) og hvor mye (alvorlighetsgrad). 

Populasjon og utvalg

Det finnes eksempler der statistikk baserer seg på hele den aktuelle befolkningen eller populasjonen, for eksempel medisinsk fødselsregister. For mange formål er det upraktisk å samle statistikk om hele populasjonen. 

Et av hovedformålene med bruk av statistikk er å trekke slutninger om en populasjon basert på et mindre utvalg. 

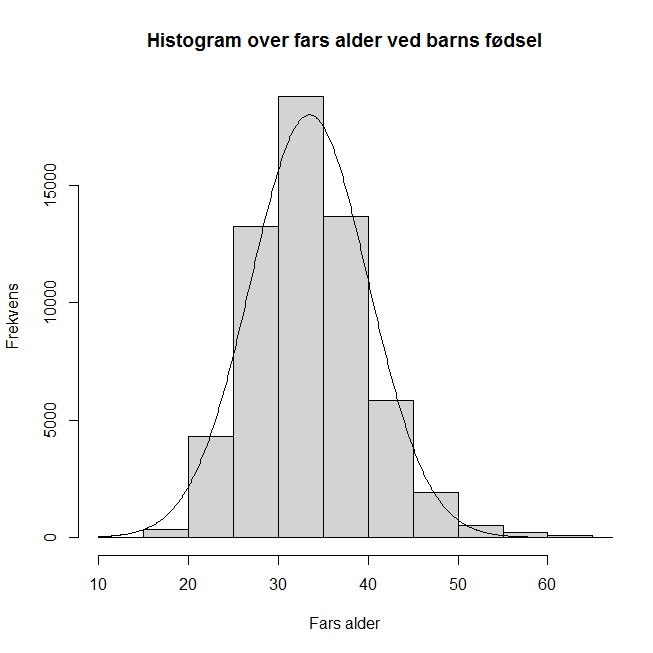
Tabell 1 – Histogram over fars alder ved barns fødsel

Histogrammet over viser alle registrerte fødsler i 2011 og hvordan nybakte fedre fordeler seg i ulike alderskategorier (Figur 1). Noen av de som ble fedre i 2011 var yngre enn 20 år og noen var eldre enn 50 år, men de fleste var mellom 30 og 35 år. Hyppigheten (frekvensen) viser hvor mange som er i hver kategori, f.eks. er 18784 nybakte fedre  (32 %) mellom 30 og 35 år.

Når vi måler alder på et stort antall mennesker vil resultatene fordele seg i en normalkurve. Normalkurven viser sentraltendens og spredning ved hjelp av gjennomsnitt (M) og standardavvik (SD). Gjennomsnittlig alder for de som ble fedre i 2011 er 33 år og standardavviket er 6.5. I eksempelet er det benyttet 11 alderskategorier à 5 år (søylebredder) og histogrammet antar en tilnærmet klokkeform (linje).

I statistikken ser vi ofte histogram med en slik klokkeform, og vi sier da at data følger en Gauss- eller normalfordelingskurve.

Normalfordelingskurven er symmetrisk, det vil si at kurven er like bratt enten man beveger seg fra midten mot venstre eller fra midten mot høyre. Slike symmetriske data dukker ofte opp i reelle situasjoner, men i den virkelige verden finnes det mange eksempler på data som ikke er normalfordelt (klokkeformet). 

Figur 2 oppsummerer norske arbeidsledighetstall fra 2012 og illustrerer skjevfordelte data som ikke passer med normalfordelingen. Når fordelingen er skjev (ikke normalfordelt) brukes vanligvis median som sentraltendens og spredning vises med interkvartil bredde (inter quartile range) eller prosentiler (percentiles). I figur 2 er medianen 10 uker, 25 % prosentilen 4 uker, 75 % prosentilen 38 uker og interkvartil bredde er 34 uker.

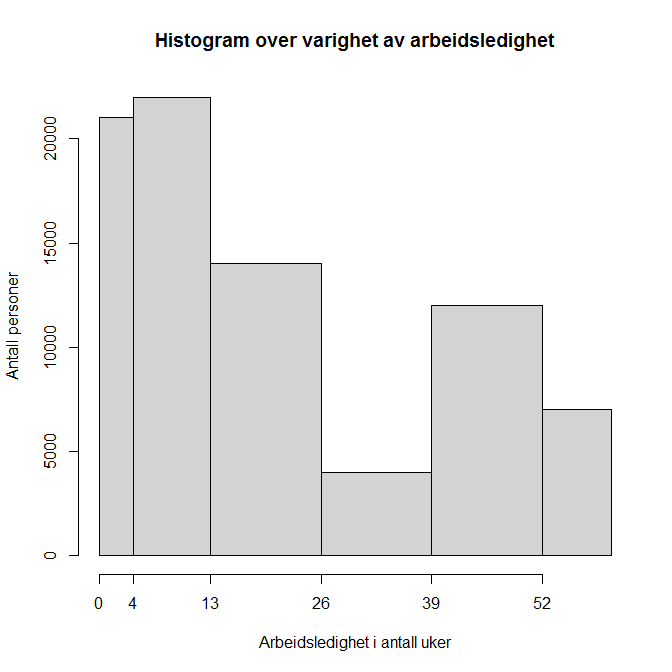
Figur 2 – Histogram over varighet av arbeidsledighet

I denne videoen laget for KBP på tvers ved Høgskulen på Vestlandet får du en enkel innføring i deskriptiv statistikk (3:42 min)

Eva Denison, Kunnskapssenteret, gir en  innføring i hvordan du kan beskrive tall. Eva underviser i statistikk og kunnskapsbasert praksis for helsepersonell. I tillegg skriver hun kunnskapsoppsummeringer m.m. og har skrevet bruksanvisninger for ulike statistikkprogram (9:30 min).