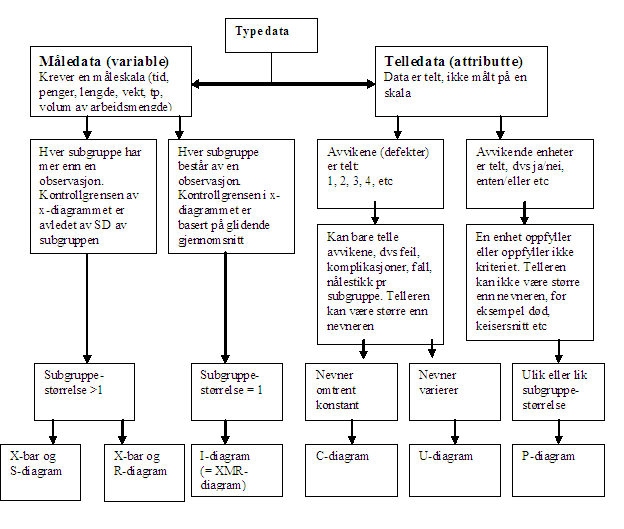
Valg av passende SPC-diagram
Det kan også gjøres mer komplisert og også mer korrekt, men det kan fort bli såpass vanskelig at mange faller av lasset. Det blir beskrevet nederst i artikkelen.
Forenklet valg
Vanligvis anbefales å skille mellom telledata og måledata når man skal velge diagramtype. Men som regel går det bra å la være dette og behandle telledata og måledata på samme måte.
Det kan være lurt først å sette dataene opp i et run-diagram, hvis type data tillater det. Ved det blir man kjent med datamaterialet sitt, diagramtypen er enkel og det gir ofte tilstrekkelig informasjon. Som regel får man imidlertid mer ut av kontrolldiagrammer, og det anbefales derfor at man også lærer seg å lage passende kontrolldiagram.
Dersom hvert datapunkt er en observasjon som for eksempel ventetid for en pasient, antall pasienter behandlet pr dag etc., velges I-diagram.
Om man har flere observasjoner i hver subgruppe (hvert datapunkt), får man mest informasjon ut av dataene dersom man lager et X-bar og S-diagram. Det er imidlertid mulig å bruke gjennomsnittet av hver subgruppe og sette det inn i et I-diagram, men da mister man informasjon om spredningen i observasjonene i hver subgruppe.
Dersom dataene er forholdstall, for eksempel et antall hendelser (teller) i forhold til totalt antall mulige hendelser (nevner), og nevnerne er større enn 12, bør P-diagram brukes. Man kan også her velge å bruke I-diagram med prosenten eller forholdstallet av hver subgruppe behandlet som en observasjon. Men dette gir mindre informasjon enn et p-diagram. Dersom nevneren er tilnærmet lik i hver subgruppe (pluss/minus 10%), får man ganske god informasjon om prosessen ved å bruke I-diagram med antall hendelser pr tidsenhet brukt som subgruppe.
Ved sjeldne hendelser brukes enten g-diagram eller datapunkter omgjort til rater (1/x) framstilt i I-diagram.
Mer komplisert valg (ikke beregnet for nybegynnere)
Etter hvert som man får mer erfaring, kan man gjøre dette mer komplisert og altså mer korrekt. Dette krever mer både av innsikt og av dataprogram, men det gir også ofte mer informasjon.
Først må man identifisere type data. Deretter konsulterer man et beslutningstre.
6.2.1 Identifisere nye data
Valg av passende kontroll-diagram starter med å identifisere type data. Det er i utgangspunktet to typer data:
- Måle-data (også kalt «continuous» eller «variable» data)
- Telle-data (også kalt «discrete» eller «attribute» data)
Måle-data kan inneha forskjellige verdier på en kontinuerlig skala (eks: ventetid i minutter, varighet av noe, kroppsvekt i gram/kg, lengde av opphold i dager etc).
Telle-data er telt, og ikke målt på en skala. Det kan være av to typer:
1. Avvikende enheter (Nonconforming units)
Avvikende enhet (defekt enhet) betyr at en enhet enten oppfyller eller ikke oppfyller et kriterium.
Disse dataene er dikotome eller binomiale – enten/eller, ja/nei-type data. Det kalles også «defective units». Telleren (for eksempel antall pasienter som falt) er en del av nevneren (antall utskrevne pas.).
2. Avvik, feil (Nonconformities)
En annen tilnærming til telledata er å telle ikke bare avvikende enheter, men alle avvik (feil/defekter). For eksempel: i stedet for å telle om en pasient har falt eller ikke i løpet av et opphold (en avvikende enhet), kan man telle hvor mange ganger en pasient har falt (avvik). Slik kan altså telleren (antall fall) bli større enn nevneren (for eksempel antall pasientdager).
Beslutningstre
Man bør så konsultere beslutnings-treet for kontroll-diagrammer (figur 21) når man skal bestemme hvilket diagram som passer best. Dette treet viser ikke alle typer kontroll-diagrammer som finnes (som for eksempel NP-diagram, G-diagram). Men de 6 diagram-typene som er tatt med (og man trenger egentlig ikke X-bar og R-diagrammet), vil være tilstrekkelige for de fleste situasjoner i helsevesenet.